1 2 3
<OPQ <POQ <QKP
Б)70° A)40° Г)20°
Объяснение:
Дано:
О - центр окружности
<МQP=70°
Установите соответствие:
1.
Рассмотрим треугольник OPQ:
OP=OQ=R ==> треугольник OPQ - равно
бедренный при основании QР.
==> <ОQP=<OPQ (как углы при основании)
==> <ОРQ=70°
2.
Рассмотрим треугольник РОQ:
OP=OQ=R ==> треугольник РОQ -равнобед
ренный при основании QP.
==> <OQP=<OPQ=70°.
По теореме о сумме углов треугольника
<РОQ=180°-( 70°+70°)=40°
3.
Рассмотрим <QKP:
Вершина угла лежит на окружности ==>
<QKP вписан в окружность и опирается
на дугу QP.
<POQ является центральным, так как
его вершина совпадает с центром ок
ружности и опирается на дугу QP.
==> по теореме о вписанных и централь
ных углах:
<QKP=1/2<POQ=1/2×40°=20°
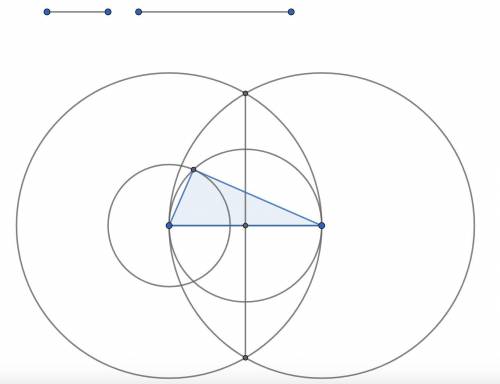
Построим прямоугольный треугольник с циркуля и линейки. Случай, когда данные стороны равны, рассматривать не будем, ибо в таком случае одна из них не может быть равна катету, а другая — гипотенузе.
1. На большей стороне (гипотенузе, назовём её b) построим две окружности с центрами в концах отрезков и радиусом b. Проведём прямую через точки пересечения окружностей. Она будет пересекать гипотенузу в середине в силу симметричности чертежа.
2. Построим окружность с центром в середине гипотенузы и радиусом b / 2. Тогда эта окружность будет содержать концы отрезка, который будет являться для неё диаметром.
3. Построим окружность с центром в одном из концов гипотенузы (не теряя общности — в левом конце) и радиусом, равному меньшей стороне (катету, назовём его a). Отметим точку пересечения с окружностью, построенной в п. 2.
4. Проведём отрезок, соединяющий правый конец гипотенузы и точку пересечения окружностей (см. п. 3). Полученный треугольник (выделен на рисунке) будет прямоугольным, так как он вписан в окружность, один из его углов опирается на диаметр, то есть угол прямой.
17 см 34 см 34 см
Объяснение:
Нехай основа х см, тоді бічні сторони по 2х см.
х+2х+2х=85
5х=85
х=17
Основа 17 см, бічні сторони по 34 см.