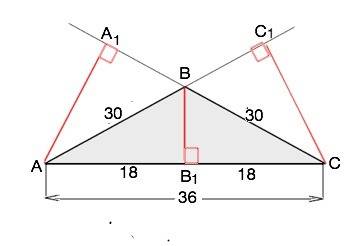
Назовём данный треугольник АВС. Он тупоугольный ( проверьте по т.Пифагора), поэтому высоты к боковым сторонам лежат за его пределами.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=36:2=18 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(30²-18²)=24 см
Высоты к боковым сторонам найдем из площади ∆ АВС.
S(ABC)=BB1•AC:2=24•18=432 см²
AA1=2S(ABC):BC
AA1=CC1=864:30=28,8 см
Биссектриса BM делит отрезок AC на отрезки AM=4 см и MC=6 см.
Есть правило о биссектрисе, делящей сторону в заданном соотношении, две оставшиеся стороны тоже находятся в этом же соотношении.
Значит AB=4x, BC=6x.
Составим уравнение: 4x+6x=25
10x=25
x=2,5.
Следовательно, AB= 4*2,5=10 см
BC=6*2,5=15 см.
ответ. 10 см и 15 см