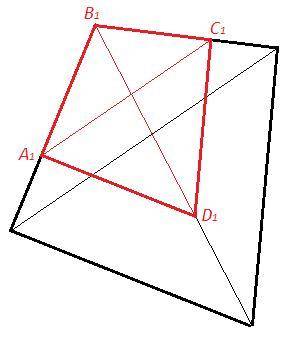
Соответствующие диагонали разбивают подобные многоугольники на подобные треугольники.
Доказываем подобие треугольников (с одинаковым коэффициентом и соответствием сторон) - тем самым доказываем подобие многоугольников.
(3) A1B1C1~ABC, A1D1C1~ADC (по двум сторонам и углу между ними)
(4) A1B1C1~ABC (по данным смежным сторонам и углу между ними)
A1D1C1~ADC (по стороне (A1C1, AC) и прилежащим углам)
(6) A1B1C1~ABC, A1B1D1~ABD (по трем пропорциональным сторонам)
∠C1A1D1=∠CAD
C1A1D1~CAD (по двум сторонам и углу между ними)
Сумма всех углов параллелограмма равна 360°.
АВСД - параллелограмм, ∠А=∠С, ∠В=∠Д
∠А+∠В+∠С+∠Д=360°
Рассмотрим условие
а)сумма двух его противоположных углов равна 94 градуса.
То есть ∠А+∠С=94°
а поскольку ∠А=∠С, значит ∠А=∠С=94°/2=47°.
∠А+∠В+∠С+∠Д=360° и ∠В=∠Д, значит
47°+∠В+47°+∠Д=360°
∠В+∠Д=360°-94°
2∠В=266°
∠В=∠Д=266°/2
∠В=∠Д=133°
ответ: при условии а) ∠А=∠С=47° и ∠В=∠Д=133°.
Рассмотрим условие
б)разность двух из них равна 70 градусов
Поскольку противоположные углы равны у параллелограмма, значит
разность противоположных углов равна 0°.
Выходит, что 70° это разность между двумя соседними углами, то есть
∠В-∠А=70°.
Допустим, что ∠А=Х°, значит
∠А=∠С=Х°
∠В=∠Д=Х°+70°
∠А+∠В+∠С+∠Д=360°
х+(х+70)+х+(х+70)=360°
4х+140°=360°
4х=220°
х=220°/4
х=55°
То есть ∠А=∠С=Х°=55°
∠В=∠Д=Х°+70°=55°+70°=125°
ответ: при условии б) ∠А=∠С=55° и ∠В=∠Д=125°