1) Нет. Биссектриса — это луч, а вершина биссектрисы — начало луча. Представь, что на нем(луче) отметили две не совпадающие точки и сравни расстояния от каждой до вершины биссектрисы. Одно будет больше другого по аксиоме измерения отрезков.
2) Да, это втрое определение биссектрисы угла, по-другому называется ее "характеристическим свойством. Его не трудно доказать. Суть заключается в том, что если ты возьмёшь любую точку на биссектрисе, кроме ее вершины, и опустишь перпендикуляры на обе стороны угла, то они будут равны.
p.s.: чел если не трудно поставь "лучшее решение")
а) ∠В = 30°, АВ=4 см, AD=ВD=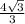
см ∠D=120°
б) S = 2√3 cм²
Объяснение:
а) Сумма острых углов прямоугольного треугольника равна 90°
∠В=90°-∠А=90°-60°=30°
Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.
⇒ АВ=2*АС=2*2=4см
По теореме Пифагора найдём катет ВС:
ВС = 2√3 см
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=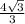
см
Так как сумма углов треугольника = 180°, то
∠АDB = 180-∠ВАD-∠В=180-30-30=120°
б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:
S = 2√3 cм²