
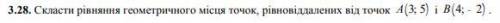
1). в
2). (рис 1) Доказываем равенство ΔCOA и ΔBOD по двум сторонам и углу между ними:
AO = OB (по условии)CO = OD (по условии)∠AOC = ∠BOD (как вертикальные углы)из этого ⇒ CA = BD = 4см
PΔCAO = CO + AO + CA = 5+3+4 = 12см
3). ABCD - параллелограмм. Поэтому ∠A=∠C по признаку параллелограмма(противолежащие углы равны)
4). тут я немного не понял. написано что ∠A и ∠C равны, потом пишут, что надо доказать что они равны...
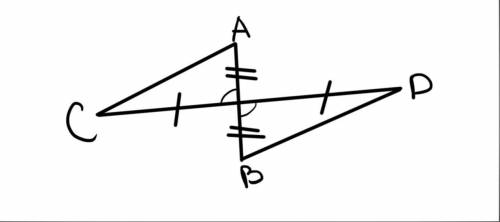
5). (рис 2) Доказываем равенство ΔABK и ΔCBM по стороне и двум прилежащих сторон:
BK = BM (по условии)∠B - общий∠BMC =∠BKA (по условии)из этого ⇒ AK = CM = 9, BC = AB = 15, CK = BC - BK = 15 - 8 = 7
AK = AO + OK = CM = MO + OC = 9 ⇒ MO = OK, AO = OC ⇒ OK + OC = 9
PΔCOK = OK + OC + CK = 9 + 7 = 16
пусть
длина медаины АА1=а
длина медины СС1=с
точка персечения О делит медианы на отрезки -свойство медиан
СО=2/3*с
ОС1=1/3*с
АО=2/3*а
ОА1=1/3*а
треугольники АОС1 и СОА1 - прямоугольные ,
т к медианы треугольника АА1 и СС1 пресекаются под углом 90 градусов
тогда по теореме Пифагора
СО^2 +OA1^2 =CA1^2 подставим сюда а , c CA1=16/2
(2/3*с)^2 +(1/3*а)^2= (16/2)^2 (1)
ОC1^2 +OA^2 =AC1^2 подставим сюда а , c AC1=12/2
(1/3*с)^2 +(2/3*а)^2= (12/2)^2 (2)
решим систему двух уравнений (1) и (2)
здесь а =4√3 с=2√33
теперь найдем сторону АС
по теореме Пифагора
АС^2= (2/3*c)^2 +(2/3*a)^2=(2/3)^2*(c^2+a*2)=(2/3)^2*((2√33)^2+(4√3)^2)=80
AC=√80 =4√5
ответ AC=4√5