4,85 ед.
Объяснение:
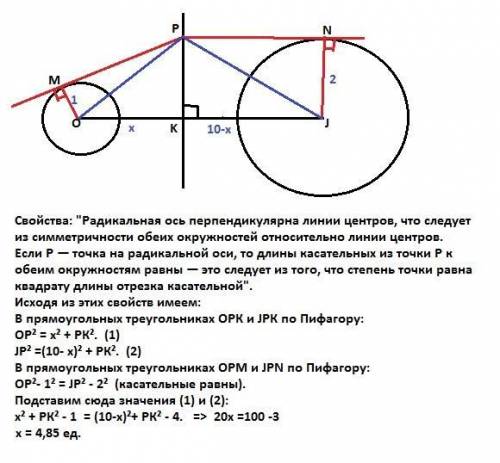
Свойства: "Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной".
Исходя из этих свойств имеем:
В прямоугольных треугольниках ОРК и JРК по Пифагору:
ОР² = х² + РК². (1)
JР² =(10- х)² + РК². (2)
В прямоугольных треугольниках ОРМ и JPN по Пифагору:
ОР²- 1² = JP² - 2² (касательные равны).
Подставим сюда значения (1) и (2):
х² + РК² - 1 = (10-х)²+ РК² - 4. => 20x =100-3.
х = 4,85 ед.
4,85 ед.
Объяснение:
Свойства: "Радикальная ось перпендикулярна линии центров, что следует из симметричности обеих окружностей относительно линии центров.
Если P — точка на радикальной оси, то длины касательных из точки P к обеим окружностям равны — это следует из того, что степень точки равна квадрату длины отрезка касательной".
Исходя из этих свойств имеем:
В прямоугольных треугольниках ОРК и JРК по Пифагору:
ОР² = х² + РК². (1)
JР² =(10- х)² + РК². (2)
В прямоугольных треугольниках ОРМ и JPN по Пифагору:
ОР²- 1² = JP² - 2² (касательные равны).
Подставим сюда значения (1) и (2):
х² + РК² - 1 = (10-х)²+ РК² - 4. => 20x =100-3.
х = 4,85 ед.

24 ед.
Объяснение:
Пусть дана трапеция ABCD.
Боковые стороны AB=30 ед., CD=40 ед.
Основания AD=90 ед., BC=40 ед.
Проведем СМ║ АВ
Тогда АВСМ - параллелограмм ( противолежащие стороны попарно параллельны.
Значит, АВ=СМ= 30 ед., ВС= АМ= 40 ед.
МD=AD-AM=90-40= 50 ед.
Рассмотрим треугольник MCD.
По теореме, обратной теореме Пифагора, треугольник MCD - прямоугольный, так как
2=2+2
50²=30²+40²
2500=900+1600
2500=2500
Высота этого прямоугольного треугольника MCD является высотой трапеции.
Найдем высоту прямоугольного треугольника. Для этого произведение катетов надо разделить на гипотенузу
CH=30×40. 1200. 12×100
= = =24
50. 50. 50
Объяснение:
ответ 24