 ,тогда все другие прямые лежат с ней в одной плоскости(аксиома) теперь среди оставшихся прямых выберем прямую
,тогда все другие прямые лежат с ней в одной плоскости(аксиома) теперь среди оставшихся прямых выберем прямую 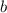 .Она лежит с прямой
.Она лежит с прямой  в одной плоскости.Но другие прямые тоже лежат с прямой
в одной плоскости.Но другие прямые тоже лежат с прямой 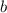 в одной плоскости(та же аксиома) и они же лежат в одной плоскости с прямой
в одной плоскости(та же аксиома) и они же лежат в одной плоскости с прямой  . по аксиоме плоскость определяется однозначно по двум пересекающимся прямым.Следовательно все оставшиеся прямые ,которые пересекаются и с
. по аксиоме плоскость определяется однозначно по двум пересекающимся прямым.Следовательно все оставшиеся прямые ,которые пересекаются и с  и с
и с 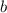 лежат в плоскости ,образованной при пересечении
лежат в плоскости ,образованной при пересечении  и
и 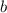 . Значит все прямые лежат в одной плоскости
. Значит все прямые лежат в одной плоскости