Question

Через две образующих конуса, угол между которыми равен α, проведена плоскость, пересекающая основание конуса по хорде, которую видно из центра основания под углом β. Радиус основания конуса равен R. Найдите: 1) площадь сечения; 2) длину образующей конуса.

Answer 1

$\boxed{AB = AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}}$

$\boxed{S_{зCAB} = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}}$

Объяснение:

Дано: OC = OB = R, ∠BOC = β, ∠BAC = α, O - центр окружности в основании конуса

Найти: AC,BC,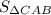 $S_{зCAB}$ - ?

Решение: Пусть точка M - середина отрезка CB. Рассмотрим треугольник ΔCOB. Треугольник ΔCOB - равнобедренный, так как по условию OC = OB = R. Проведем отрезок OM. Так как по построению CM = MB, то по определению MO - медиана равнобедренного треугольника ΔCOB. Так как CB - основание треугольника ΔCOB

(по условию OC = OB = R), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда ∠COM = ∠BOM = ∠BOC : 2 = β : 2 = 0,5β. Так как OM - высота, то треугольник ΔMOB - прямоугольный. Рассмотрим треугольник ΔMOB.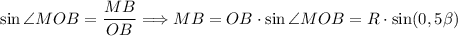 $\sin \angle MOB = \dfrac{MB}{OB} \Longrightarrow MB = OB \cdot \sin \angle MOB = R \cdot \sin (0,5\beta )$.

Рассмотрим треугольник ΔCAB. Треугольник ΔCAB - равнобедренный, так как по условию AC = AB как образующие конуса. Проведем отрезок AM. Так как по построению CM = MB, то по определению MA - медиана равнобедренного треугольника ΔCAB. Так как CB - основание треугольника ΔCAB (AC = AB как образующие конуса), то по теореме медиана проведенная к основания равнобедренного треугольника является биссектрисой и высотой, тогда

∠CAM = ∠BAM = ∠BAC : 2 = α : 2 = 0,5α. Так как AM - высота, то треугольник ΔMAB - прямоугольный. Рассмотрим треугольник ΔMAB.

$\sin \angle MAB = \dfrac{MB}{AB} \Longrightarrow AB = \dfrac{MB}{\sin \angle MAB} = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$.

Так как AC = AB как образующие, то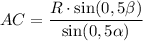 $AC = \dfrac{R \cdot \sin (0,5\beta)}{\sin (0,5\alpha )}$.

По формуле площади для треугольника ΔBAC:

$S_{зCAB} = 0,5 \cdot AC \cdot AB \cdot \sin \angle BAC = \dfrac{0,5 \cdot R^{2} \cdot \sin^{2} (0,5\beta) \cdot\sin \alpha }{\sin^{2} (0,5\alpha )}$.