Т.к. сторона АВ делится как 3:2, то АМ=3х, МВ=2х.Для решения задачи проведите радиусы окружности в точки касания, обозначьте точки буквами: на стороне АВ - М, на стороне ВС -N, на АС -F. Радиусы, проведенные в точку касания перпендикулярны касательной. Получаются прямоугольные треугольники МВО и ВОN. Эти треугольники равны по катету и гипотенузе.Значит, МВ=ВN=2х. Аналогично АМ=АF=3х, СN=CF=5. Периметр-это сумма длин всех сторон треугольника: 3х+3х+2х+2х+5+5=30
10х=20, х=2. Подставляя, получаем, что АС=11см.
Сначала правило. В прямоугольнике диагонали равны. Тогда: если через вершину С проведём параллельную ДВ до пересечения с прямой АВ и соеденим точки МС, то получим параллелограм ДВМС, в котором ВД=СМ+ 8 см Сейчас если проведём параллелную прямую через продолжение СВ с пересечением в точке N получим тр-к СNМ и САN. Стороны АС парал МN , АМ перп СN. Фигура АСМN Является ромбом у которого все стороны равны и одна из сторон опирается на диагональ АС прямоугольника АВСД Которая равна 8см. Периметр АСМN равен 32 см
Объяснение:
Дано:
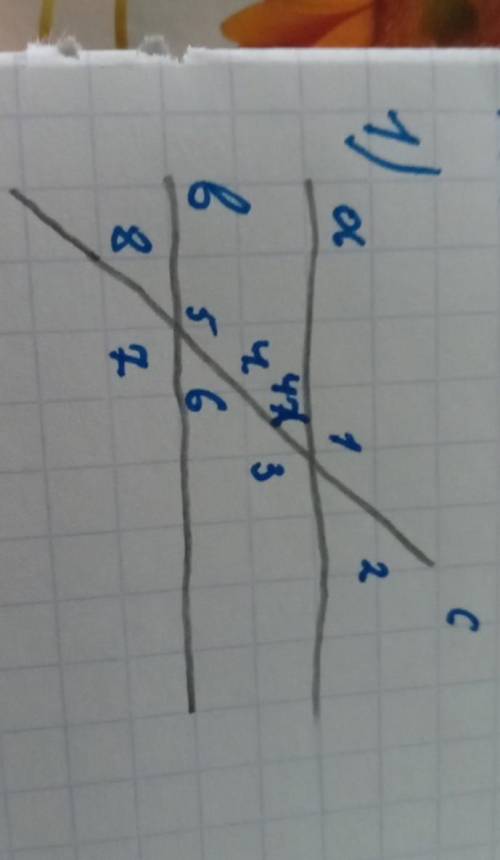
Параллельные прямые.
<4=47°.
Найти: все углы.
<4=<2=47°, так как вертикальные углы.
<1+<2=180°, так как смежные углы.
<1=180°-47°=133°.
<1=<3=133°, так как вертикальные углы.
<3+<6=180°, так как соответственные углы.
<6=180°-133°=47°
<6=<8=47°, так как вертикальные углы.
<8+<7=180°, так как смежные углы.
<7=180°-47°=133°
<7=<5=133°, так как вертикальные углы.