
(см. объяснение)
Объяснение:
1)
Тебя просят найти боковую сторону. У тебя есть ее часть. Значит найти нужно другую ее часть.
Пусть x - неизвестная часть боковой стороны.
Тогда высота треугольника равна:
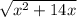 (по теореме Пифагора)
(по теореме Пифагора)
И соответственно основание равно:
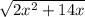
С другой стороны основание равно:
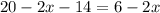
Получили уравнение:
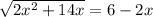
Откуда находим x=1.
Тогда вся сторона равна 8.
2)
Вспомним формулу:
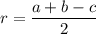 ,
,
где a и b - катеты треугольника BDC, а c - гипотенуза.
Найдем a+b:
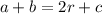
Вспомним формулу:
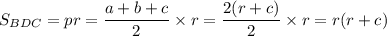
Это площадь треугольника BDC.
Тогда площадь ABC:
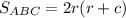
Подставим в формулу значения из дано и получим ответ:
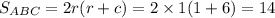
(см. объяснение)
Объяснение:
1)
Тебя просят найти боковую сторону. У тебя есть ее часть. Значит найти нужно другую ее часть.
Пусть x - неизвестная часть боковой стороны.
Тогда высота треугольника равна:
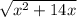 (по теореме Пифагора)
(по теореме Пифагора)
И соответственно основание равно:
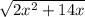
С другой стороны основание равно:
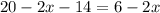
Получили уравнение:
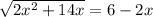
Откуда находим x=1.
Тогда вся сторона равна 8.
2)
Вспомним формулу:
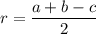 ,
,
где a и b - катеты треугольника BDC, а c - гипотенуза.
Найдем a+b:
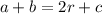
Вспомним формулу:
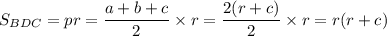
Это площадь треугольника BDC.
Тогда площадь ABC:
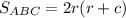
Подставим в формулу значения из дано и получим ответ:
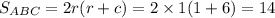
Объяснение:
Дано: AB = 3, ,
,  ,
,  , ∠MAC > 90°
, ∠MAC > 90°
Найти: cos ∠MAC - ?
Решение: По теореме косинусов для треугольника ΔABC:
Так как по условию треугольник , то по свойствам подобных треугольников их соответствующие углы равны. Так как в треугольнике только 1 угол может быть может быть тупым, то угол ∠ABC > 90°, так как cos ∠ABC < 0. Тогда ∠ABC = ∠MAC, следовательно cos ∠ABC = cos ∠MAC =
, то по свойствам подобных треугольников их соответствующие углы равны. Так как в треугольнике только 1 угол может быть может быть тупым, то угол ∠ABC > 90°, так как cos ∠ABC < 0. Тогда ∠ABC = ∠MAC, следовательно cos ∠ABC = cos ∠MAC =  .
.