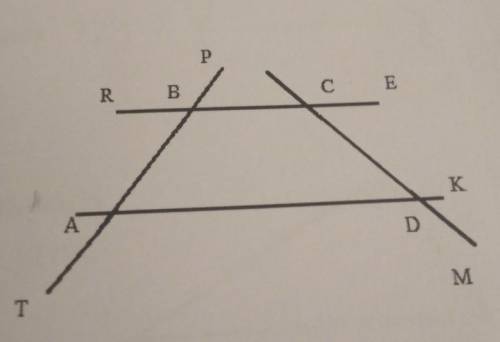
Объяснение:
а) ∠РВС=∠BAD=70° как соответственные углы
б) ∠RBA=∠BAD=70° как накрест лежащие углы
в) ∠АВС=180-70=110° как односторонние углы
Косинус угла отрицателен, значит угол между векторами АВ и ВС (это угол А) и противолежащий ему угол С тупые.
Пусть нам дана трапеция ABCD, где BC||AD, а угол ABC = углу BCD и они окажутся больше, чем 90 градусов...
Треугольник ABC- равнобедренный и угол BAC= углу BCA;
А диагональ AC является секущей между параллельными линиями BC и AD, значит угол CAD= углу BCA и. конечно же, равен углу ADC, как тогда угол ACD=углу BAC + угол BCA...
И тогда что у нас выходит:
Возьмём неизвестное за ''икс'', т.е. введём переменную:
Пусть угол BAC = x, и тогда угол ACD=2x и угол BCD=3x, а из этого следует и угол ABC=3x
Угол CAD=2x и угол ACD тоже равен 2x
Вообще, мы можем получить, что
3x+3x+2x+2x=360 градусов;
10x=360 => x= 36 градусов;
Ну т. е. угол ABC = углу BCD = 108 градусов;
угол BAD = углу CDA=72 градуса.
Мы определили углы трапеции,
Теперь остаётся записать лишь ответ: 72, 108, 108, 72 - искомые углы.
Задача решена.
при ВС║АD и секущей АВ углу ВАD
а) соответственный ∠РВС=70° (равны по свойству)
б) накрест лежащий ∠RBA=70° (равны по свойству)
в) односторонний ∠ АВС=180°-70°=110° ( т.к.в сумме составляют 180°)