
1)
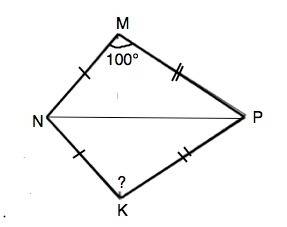
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
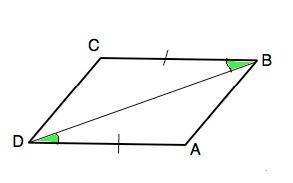
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
Объяснение:
8)
а=5см
Р=17см.
b=?
Решение
В равнобедренном треугольнике боковые стороны равны.
Р=а+2b →
b=(P-a)/2=(17-5)/2=12/2=6см
ответ: 6см.
9)
∆АBD=∆CBD,
Доказательство:
АВ=СD, по условию
АD=BC, по условию
ВD- общая сторона треугольников ∆АВD; ∆СВD.
∆ABD=∆CBD, по третьему признаку (ССС)
Что и требовалось доказать
В равных треугольниках соответственные углы равны.
<А=<С