
Объяснение:
координаты вектора вычисляются так: из соответствующей координаты конца вектора нужно вычесть соответствующую координату начала вектора.
получим координаты вершин параллелограмма, выраженные через координаты одной точки (точки А, например)
координаты векторов-диагоналей параллелограмма вычисляются аналогично...
косинус угла между векторами = частному от деления скалярного произведения векторов на произведение длин векторов.
скалярное произведение векторов=сумме произведений соответствующих координат.
длина вектора=корню квадратному из суммы квадратов координат (т.Пифагора)
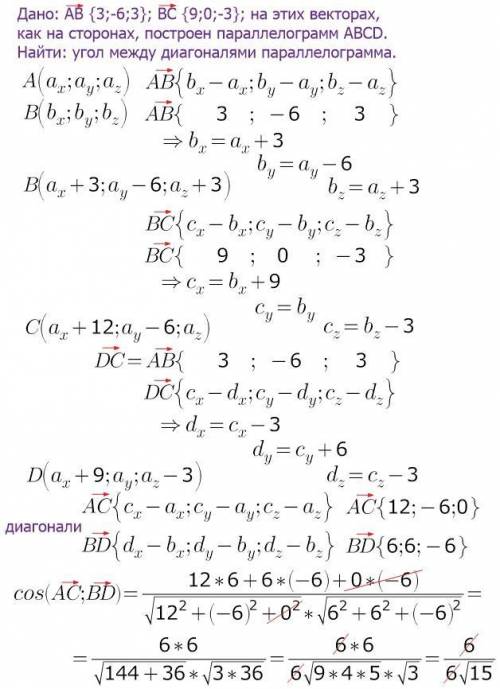
x²+ (y –65/18)² = 29/1
Объяснение:
Центр окружности имеет координаты О (0;уо) .
Точки, принадлежащие окружности имеют координаты (4;0) и (0;9). Их координаты удовлетворяют уравнению окружности:
x²+ (y – у₀)² = R² , где (0;у₀)-координаты центра .
х²+(0- у₀)²=R² , или 16 +у₀²=R²
х²+ (y- у₀)²=0²+(9- у₀)² или 81-18у₀+ у₀²= R² Вычтем из 1 уравнения 2. Получим :
16-81+18 у₀=0
18 у₀=65
у₀=3,6. Центр имеет координаты О (0; 3,6).
Найдем R²=(4²+(0-3,6)² )= 29. R=5,4
x² + (y – 21,7)² =29