цилиндр АВСD.
BD = 10 см.
∠BDС = 60˚
Найти:D - ?
Решение:Осевое сечение цилиндра это прямоугольник.(т.к. основания цилиндра равны и параллельны и образующие цилиндра равны и параллельны друг другу)
При пересечении цилиндра плоскостью, параллельной оси цилиндра т.е. перпендикулярной основанию, также получается прямоугольник.
Диагональ BD образует прямоугольный △СBD
Сумма острых углов прямоугольного треугольника равна 90°.
=> ∠DBC = 90˚ - 60˚ = 30˚
Если угол прямоугольного треугольника равна 30°, то напротив лежащий катет равен половине гипотенуза.
=> BD = 2DC
DC = 10/2 = 5 см
DC - и есть диаметр основания D этого цилиндра.
ответ: 5 см.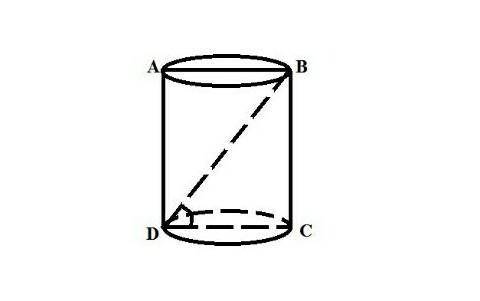
ΔABC - равнобедренный;
высота BD = 6,4 см;
AB = BC = 12,8 см.
Найти:∠A = ?°; ∠B = ?°; ∠C = ?°.
Решение:Высота, проведённая к основанию равнобедренного треугольника, является и медианой, и биссектрисой.
⇒ AD = DC, ∠ABD = ∠BDC (по выше указанному свойству).
⇒ ΔABD = ΔCBD (по двум сторонам и углу между ними).
Нам также известно что равные треугольники прямоугольные (высота BD).
Если катет равен половине гипотенузы, то напротив лежащий угол составляет 30°.
Боковые стороны равнобедренного ΔABC - гипотенузы прямоугольных ΔABD и ΔСBD, а высота - общий катет.
Как мы уже отметили, этот общий катет равен половине гипотенузы, так как 6,4 * 2 = 12,8 см. Поэтому ∠A = ∠C = 30°.
Сумма острых углов в прямоугольном треугольнике равна 90°.
⇒ ∠ABD = ∠CBD = 90° - 30° = 60°. ⇒ ∠B = 120°.
ответ: ∠A = ∠C = 30°, ∠B = 120°.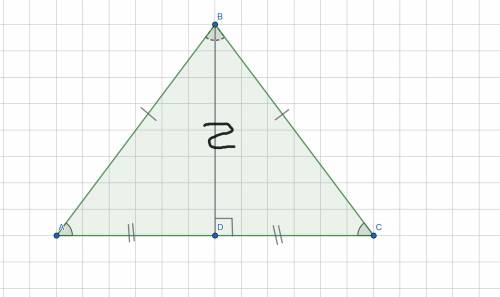
пусть диагонали ромба пересекаются в точке О. рассмотрим ΔАОВ:<АОВ=90. АВ-гипотенуза=10см(по условию), ВО=8 см(по условию диагональ ВД=16см)
по теореме Пифагора:АВ^2=ВО^2+АО^2.
10^2=8^2+АО^2. АО^2=100-64. АО=√36, АО=6, АС=6*2=12
т.к. ВВ1 перпендикулярно ВС и АВ, то ВВ1 перпендикулярно плоскости ромба. следовательно, АА1 также перпендикулярна плоскости ромба(если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости). АА1 перпендикулярна диагонали АС(прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой в этой плоскости).
рассмотрим ΔА1АС: <А1АС=90, АА1=13 см(по условию), АС=12 см. по теореме Пифагора: А1С^2=АА1^2+АС^2. 13^2=АА1^2+12^2? АА1=√169-144, АА1=√25, АА1=5