
По теореме:. Если прямая (ВС), не лежащая в данной плоскости (сечения), параллельна какой-нибудь прямой (МК), лежащей в этой плоскости, то она параллельна самой плоскости. Проведем МК║ВС и получим линию пересечения плоскостей грани и сечения.
На грани АDC теперь есть вторая точка, принадлежащая линии пересечения плоскости сечения и грани. Соединим их.
S = √3 ед².
Объяснение:
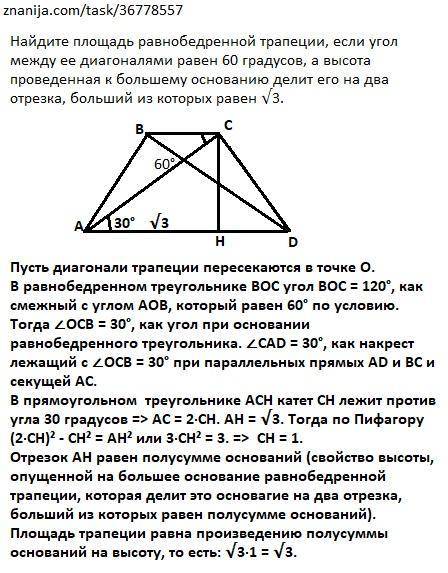
Пусть диагонали трапеции пересекаются в точке О.
В равнобедренном треугольнике ВОС угол ВОС = 120°, как смежный с углом АОВ, который равен 60° по условию. Тогда ∠ОСВ = 30°, как угол при основании равнобедренного треугольника. ∠CAD = 30°, как накрест лежащий с ∠ОСВ = 30° при параллельных прямых AD и ВС и секущей АС.
В прямоугольном треугольнике АСН катет СН лежит против угла 30 градусов => АС = 2·СН. АН = √3. Тогда по Пифагору
(2·СН)² - СН² = АН² или 3·СН² = 3. => СН = 1 ед.
Отрезок АН равен полусумме оснований (свойство высоты, опущенной на большее основание равнобедренной трапеции, которая делит это основание на два отрезка, больший из которых равен полусумме оснований). Итак, полусумма оснований равна √3 (дано). Тогда площадь трапеции равна произведению полусуммы оснований на высоту, то есть: √3·1 = √3 ед².
<1=102°
<2=78°
<3=102°
<4=78°
<5=102°
<6=78°
<7=102°
<8=78°
Объяснение:
<3+<2=180°, смежные углы
Пусть градусная мера угла <2 будет х°; тогда градусная мера угла <3 будет (х+24)°
Уравнение
х+(х+24)=180
2х=156
х=78° градусная мера угла <2
78+24=102° градусная мера угла <3.
<3=<1, вертикальные углы
<1=102°
<3=<5, внутренние накрест лежащие
<5=102°
<3=<7, соответственные углы
<7=102°
<2=<4, вертикальные углы
<4=78°
<2=<8, внутренние накрест лежащие
<8=78°
<2=<6, соответственные углы
<6=78°