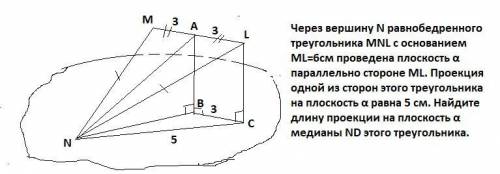
Через вершину N равнобедренного Δ MNL с основанием ML=6см проведена плоскость α параллельно стороне ML. Проекция одной из сторон этого треугольника на плоскость α равна 5 см. Найдите длину проекции на плоскость α медианы ND этого треугольника.
Объяснение:
Проекцией, равной 5 см , не может быть сторона ML=6 , т.к. ML║α .
Пусть LC, АВ -перпендикуляры к плоскости α. Тогда LC=AB. тк ML║α .
Проекцией стороны NL на плоскость α будет отрезок NC=5 см( отрезок между основанием перпендикуляра и основанием наклонной) , а проекцией медианы NA будет отрезок NB.
МА=АL=3 см . АВСL-прямоугольник , поэтому ВС=3 см,
Т.к медиана NB равнобедренного ΔNCO, является высотой , то ΔNBC- прямоугольный , по т. Пифагора NB=√(5²-3²)=4 (см).
Объем конуса находят по формуле: V = 1/3 · Sосн · H, где Sосн - площадь основания, H - высота. В основании - круг, Sосн = πR², где R - радиус основания.
Пусть дан конус (см. рис.) . SО - высота, SВ - образующая, ОВ - радиус. По условию SО : SВ = 4 : 5 и V = 96π см³.
ΔSОВ - прямоугольный. Если принять, что SО = (4х) см, SВ = (5х) см, то по теореме Пифагора ОВ² = SВ² - SО² = (5х)² - (4х)² = 25х² - 16х² = 9х², откуда, учитывая, что длины сторон положительны, ОВ = 3х (см).
Подставляем полученные выражения в формулу объема:
V = 1/3 · πR² · H = 1/3 · π · ОВ² · SО = 1/3 · π · (3х)² · 4х = 12πх³ = 96π, т.е.
12πх³ = 96π,
х³ = 8,
х = 2.
Тогда ОВ = 3 · 2 = 6 (см), SB = 5 · 2 = 10 (см).
Площадь полной поверхности конуса равна:
Sполн = Sосн + Sбок = πR² + πRL = πR(R + L), где R - радиус основания, L - образующая конуса.
Значит, Sполн = π · ОВ · (ОВ + SВ) = π · 6 · (6 + 10) = 6π · 16 = 96π (см²).
ответ: 96 см².

площадь параллелограмма равна AD*BE
отсюда AD=Sabcd:BE
AD=70:7=10 см
AD=ED+AE
AE=AD-ED=10-7=3см