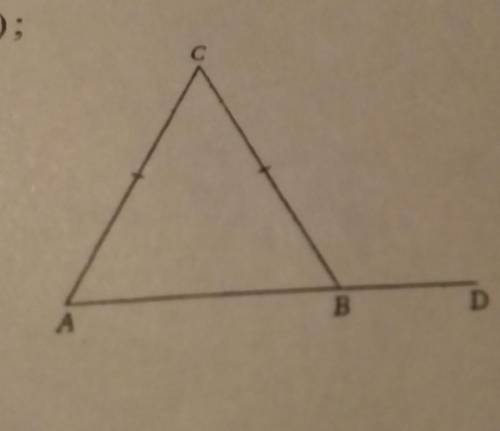
Дано:
треугольник ABC: AC=BC; ∠а = 52°.
Найти:
∠CBD - ?
1) Найдем другие углы треугольника ABC
Так как треугольник АВС - равнобедренный (по условию)
∠а = ∠b = 52°.
∠c = 180° - ∠а - ∠b = 180° - 52° - 52°.
∠c = 76°.
2) Найдем ∠CBD:
Так как внешний ∠ равен сумме двух углов треугольника, не смежных с ним, получим уравнение:
∠CBD = ∠а + ∠c = 52° + 76° = 128°.
ответ: ∠CBD = 128°.

треугольник АВС, АН=30 и СМ=39 медианы, АМ=МВ, ВН=НС, МН-средняя линия треугольника=1/2АС=26/2=13, АМНС - трапеция, МН параллельна АС, из точки Н проводим линию параллельную СМ до пересечения ее с продолжением АС в точке Е, ЕН=СМ=39, СМНЕ- параллелограмм, СЕ=МН=13, АЕ=АС+СЕ=26+13=39
треугольникАНЕ равнобедренный, АЕ=ЕН=39, проводим высоту ЕТ=медиане=биссектрисе на АН, АТ=ТН=1/2АН=30/2=15, треугольникАТЕ прямоугольный, ЕТ²=АЕ²-АТ²=1521-225=1296, ЕТ=36, площадь АНЕ=площадь трапеции АМНС=1/2*АН*ЕТ=1/2*30*36=540, что составляет 3/4 площади АВС
(площадь треугольника отсекаемого средней линией (МН)=1/4 площади АВС, можно подсчитать самим),
площадь АВС=площадьАМНС*4/3=540*4/3=720
угол CBD=128°
Объяснение:
угол А=углу СВА=52°(углы при основании в равнобедренном треугольнике равны)
угол CBD=180°-52°=128°(как смежные углы(сумма смежных углов равна 180°))