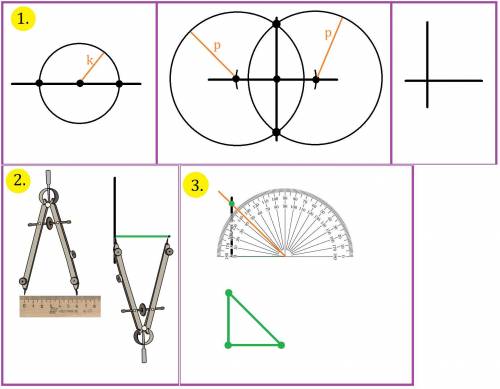
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.
Проведём 2 перпендикулярные прямые (см. рис. 1). Для этого:
1. Из точки на произвольной прямой, проведём окружность произвольного радиуса k.
2. В точках пересечения окружности с прямой, проведём окружности с радиусом p, при это p > k.
3. Через точки пересечений окружностей проводим прямую, она будет перпендикулярна первой прямой.
С циркуля замерим на линейке 6 см и отложим 6 см на одной стороне прямого угла (см. рис. 2).
С транспортира отложим угол в 45° и соединим точки, как показано на рис. 3. Получили искомый треугольник.

Відповідь:
Пояснення:
Маємо пряму АВ, будуємо пряму АА3 довільної довжини. Так як нам треба розділити АВ на три частини в співвідношенні 2:3:4, то АА3 краще взяти довжиною кратне 9, маємо 9 частин 2+3+4.
Пряму АА3 ділемо на 3 частини довжиною 2, 3, 4 см відповідно
Зєднуємо кінці відрізків В і А3
Будуємо паралельні прямі А1В1 || А2В2 || А3В
за теоремою про пропорційні відрізки, наслідки теореми Фалеса, відрізки АВ1:В1В2:В2В=2:3:4