Найдите площадь треугольника abc,у которого bc=6 см, ab=12 корень из 2 см,а угол b равен 45 градусов. - id210368220221028 от vadimmatus 28.10.2022 06:12

Question

Геометрия: Найдите площадь треугольника abc,у которого bc=6 см, ab=12 корень из 2 см,а угол b равен 45 градусов. варианты ответов а)3 см2; б)36 см2; в) 72 см2; с)правильный ответ отличен от указанных .

vadimmatus · Accepted Answer

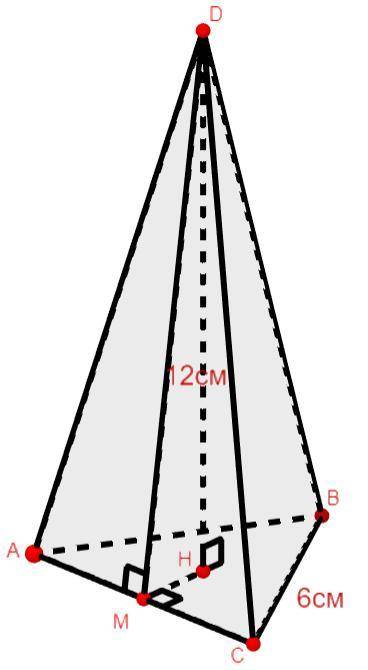
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.

S(осн.)= $S_{ABC}=\dfrac{AB^2\sqrt3}{4} =\dfrac{36\sqrt3}{4}$ =9√3 см².

Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.

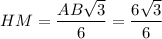$HM=\dfrac{AB\sqrt3}{6} =\dfrac{6\sqrt3}{6}$ =√3 см

В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.

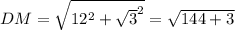$DM=\sqrt{12^2+\sqrt3 ^2} =\sqrt{144+3}$ =√147 см

Боковые грани правильной пирамиды это равные треугольники.

S(бок.)= $3\cdot S_{ADC} =3\cdot DM\cdot AC\cdot \dfrac12 =\dfrac32 \cdot 6\cdot \sqrt{147}$ =9√147 см²

S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²

ответ: 9√3 + 9√147 см².

Вправильной треугольной пирамиде сторона основания равна 6 см, а высота пирамиды равна 12см. вычисли

MOGZ ответил