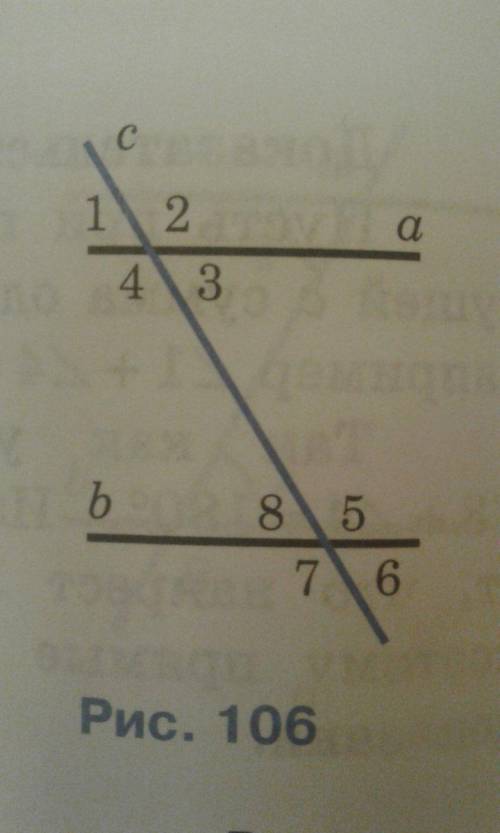
Треугольники А0Д и В0С - подобные (уг.В0С = уг.А0Д как вертикальные; уг.СВ0 = уг.АД0 как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей ВД).
Площадь тр-ка ВОС равна S1 = 0,5ВС·Н1
Площадь тр-ка АОД равна S2 = 0,5АД·Н2
При этом Н1:Н2 = к -коэфиициент подобия, а S1 : S2 = к²
S1 : S2 = 0,5ВС·Н1 : 0,5АД·Н2
к² = к· ВС: АД
к = 9/16
Итак, нашли коэффициент подобия.
Из подобия тех же тр-ков следует, что ОВ:ОД = 9/16, но ОД = АС - ОВ и
ОВ: (АС - ОВ) = 9/16
16·ОВ = 9·(АС - ОВ)
16·ОВ = 9·АС - 9·ОВ
25·ОВ = 9·АС
ОВ = 9·АС/25 = 9·18:25 = 6,48
ответ: ОВ = 6,48см
ответ: 5 см
Объяснение:
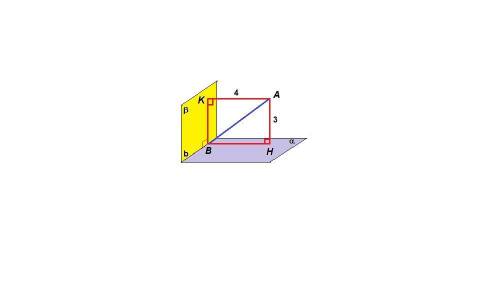
Пусть двугранный угол образован перпендикулярными плоскостями α и β, которые пересекаются по прямой b.
Так как расстояние от точки до плоскости - длина перпендикуляра, проведенного из точки к плоскости, проведем АН⊥α и АК⊥β.
АН = 3 см - расстояние от точки А до плоскости α
АК = 4 см - расстояние от точки А до плоскости β.
Докажем, что плоскость (АКН) перпендикулярна ребру двугранного угла - прямой b:
АН⊥α, b ⊂ α, ⇒ AH⊥b
AK⊥β, b ⊂ β, ⇒ AK⊥b,
так как прямая b перпендикулярна двум пересекающимся прямым плоскости (АКН), то она перпендикулярна плоскости.
Пусть плоскость (АКН) пересекает прямую b в точке В.
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости:
b⊥AB, b⊥KB и b⊥HB.
Из этого следует, что
АВ - искомое расстояние от точки А до ребра двугранного угла (длина перпендикуляра из точки к прямой),∠КВН = 90° - линейный угол двугранного угла.В четырехугольнике АНВК три угла прямые, значит и четвертый так же прямой, АНВК - прямоугольник, противоположные стороны равны.
По теореме Пифагора из прямоугольного треугольника АВК:
АВ = √(АК² + ВК²) = √(16 + 9) = √25 = 5 см
Объяснение:
а) ∠1=37° , ∠7= 143°;
∠7 и ∠8 - смежные углы. Их сумма 180°,
⇒∠8=180°-∠7=180°-143°=37°
⇒ ∠1=∠8=37°
∠1 и ∠8 - соответственные углы при двух прямых а и b и секущей с
Если соответственные углы равны, то прямые параллельны⇒ а ║ b
б) ∠1= ∠6
Но ∠6=∠8 - как вертикальные углы при двух пересекающихся прямых b и с.
⇒∠1=∠8
∠1 и ∠8 - соответственные углы при двух прямых а и b и секущей с, а если соответственные углы равны, то прямые параллельны.
⇒ а ║ b
в) ∠1 = 45°, а ∠7 в три раза больше ∠3
∠1=∠3 - как вертикальные углы при двух пересекающихся прямых а и с.
⇒ ∠3=45°. ∠7=3*45°=135°
∠7 и ∠8 - смежные углы. Их сумма 180°,
⇒∠8=180°-∠7=180°-135°=45°
⇒∠1 = ∠8 = 45°
∠1 и ∠8 - соответственные углы при двух прямых а и b и секущей с
Если соответственные углы равны, то прямые параллельны⇒ а ║ b