√7 м.
Объяснение:
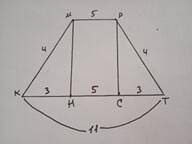
Дано: КМРТ - трапеция, МР=5 м, КМ=РТ=4 м, КТ=11 м. МН - ?
Проведем высоты МН и РС.
Тогда СН=МР=5 м, КН=СТ=(11-5):2=3 м, т.к. ΔКМН=ΔТРС по катету и гипотенузе.
ΔКМН - прямоугольный, МН=√(4²-3²)=√(16-9)=√7 м.
ответ:Дан ромб АВСД. диагональ АС пересекает ВД в т.О
АС-меньная диагональ.УголВ=углу Д=60градусов.
Диагонали ромба делят углы пополам=> уголАДО=60:2=30градусов
диагонали ромба перпендикулярны => треугольник АОД прямоугольный.
Катет, лежащий напротив угла 30 градусов равен половине гипотенузы => АО=49:2=24,5
Диагонали ромба точкой пересечения делятся пополам => АС=2*АО=2/24,5=49
Можно и другим
Треугольник АСД - равносторонний, т.к. он равнобедренный (АД=ДС по св-вам ромба), углы при основании равны, а третий угол =60градусов => углы при основании тоже по 60 градусов => АД=АС=49
Объяснение:
ответ: ∠DBE=15*.
Объяснение:
"ABCD-это ромб, а точка E находится на стороне DC так, что(<BEC) = 55°. Если m(<A)=100°, найдите m(<DBE).
Треугольник DВЕ - равнобедренный (углы у основания равны).
∠А+∠ABD+∠BDA=180*;
∠DBA=∠BDA=(180*-100*)/2=40*;
***
В треугольнике BDE ∠BDE=40*, a ∠BED=180*-55*=125*.
Значит ∠DBE=180*-(40*+125*) =15*.
ответ: ∠DBE=15*.
***
На английском:
The triangle DBE is isosceles (the angles at the base are equal).
∠A+∠ABD+∠BDA=180*;
∠DBA=∠BDA=(180*-100*)/2=40*;
***
In the triangle BDE ∠BDE=40*, a ∠BED=180*-55*=125*.
Means ∠DBE=180*-(40*+125*) =15*.
Answer: ∠DBE=15*.
проведём две высоты. получим прямоугольник с одной стороной равной высоте, второй рукой меньшему основанию
ТК трапеция равнобедренная, то отрезки заключённые между высотой и боковой стороной равны. высчитаем их ((11-5)/2=3)
по теореме Пифагора находим высоту
x=sqrt(4-3)*(4+3)=sqrt(7)
sqrt- корень квадратный