

Теоремы (свойства параллелограмма):
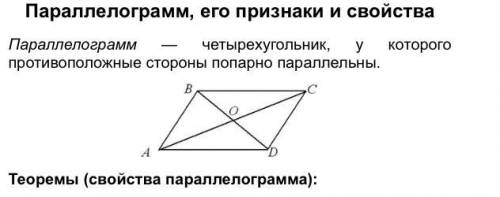
В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle
ADC,\angle BAD = \angle BCD.
Диагонали параллелограмма точкой пересечения делятся пополам: AO
= OC, OB = OD.
Углы, прилежащие к любой стороне, в сумме равны 180^\circ .
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.
Движение переводит плоскость в плоскость.
Докажем это свойство. Пусть a - произвольная плоскость. Отметим на ней любые три точки A, B, C, не лежащие на одной прямой. Проведем через них плоскость a'.
Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a'.
Пусть X - произвольная точка плоскости a. проведем через нее какую-нибудь прямую a в плоскости a, пересекающую треугольник ABXC в двух точках Y и Z. Прямая а перейдет при движении в некоторую прямую a'. Точки Y и Z прямой a перейдут в точки Y' и Z', принадлежащие треугольнику A'B'C', а значит, плоскости a'.
Итак прямая a' лежит в плоскости a'. Точка X при движении переходит в точку X' прямой a', а значит, и плоскости a', что и требовалось доказать.
В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.
III. Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.