Объяснение:
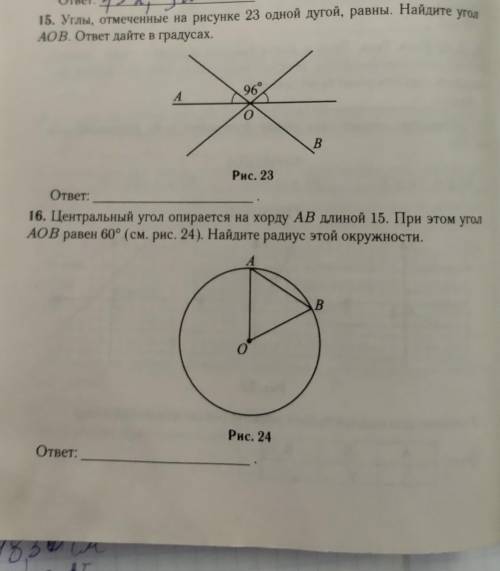
15. отмеченный угол - (180-96)/2=42°;
∡АОВ=96+42=138° (сумма двух вертикальных углов).
16. ΔАОВ равнобедренный (АО, ВО радиусы) ⇒ ∡А=∡В=(180-60)/2=60° ⇒ ΔАОВ равносторонний ⇒АО=АВ=15 ед.
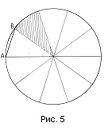
! На примере вложенного рис. постараюсь объяснить смысл записи(отношения):
2:3:4.
Если мы обозначим правый конец диаметра точкой С, то дуга АВ составит 1 часть ( из 10 равных),ВС- 4 части, СА- 5 частей, Для краткости это запишется 1:4:5.Каждая названная дуга имеет градусную меру и её величина зависит от меры одной части, принято град. меру одной части брать за х, тогда отношение 1:4:5
будет выглядеть 1х:4х:5х, в "сумме" эти дуги образуют окружность,
т.е. 1х+4х+5х=360⁰
10х=360⁰
х=36⁰, а значит АВ=36⁰,ВС=36⁰·4=..., АС= 180⁰.
1) Аналогично решается Ваша задача.
Пусть одна часть х⁰, тогда 2х+3х+4х=360⁰
9х=360⁰
х=40⁰
Таким образом , градусные меры дуг 80⁰,120⁰,160⁰.
Учитывая, что углы тр-ка являются вписанными, то их град. мера в 2 раза меньше град. меры дуги на ,которую опираются.Значит углы тр-ка равны:
40⁰; 60⁰;80⁰.
Меньшая диагональ равна 12, значит половина равна, 6
Так же угол в 60 градусов делится диагональю(биссектрисой) значит половина угла равна 30
* угол в 30 градусов лежит против половины маленькой диагонали
Та как против угла в 30 градусов лежит угол в 2 раза меньше гипотенузы
тогда гипотенуза равна 12 см, а значит периметр треугольника равен Рассмтрим треугольник который лежит выше маленькой диагонали
Он равнобедренны по определению ромба
А занчит улы при основании равны, т.к. вершина равна 60 градусам то и остальные углы тоже по 60 значит стороны ромба равны по 12 см так-ка треугольник равносторонний, значит периметр равен 48 градусов
15. 138°; 16. 15;
Объяснение:
15.
Пусть х - градусная мера угла, обозначенного одной дугой, тогда развёрнутый угол, равный 180°, состоит из угла, равного 96°. и двух углов по х°.
Найдём угол х:
180° = 96° + 2х
2х = 84°
х = 42²
Угол АОВ равен вертикальному углу, состоящему из угла 96° и угла х = 42°, поэтому
∠АОВ = 96° + 42° = 138°.
16.
На рисунке ОА = ОВ = R - радиус окружности.
Следовательно, Δ АОВ - равнобедренный и
∠А = ∠В = 0,5 · (180° - ∠АОВ) = 0,5 · (180° - 60°) = 60°.
Все внутренние углы треугольника АОВ равны между собой, следовательно, ΔАОВ - равносторонний, и радиус окружности
ОА = ОВ = AB = R = 15.