
∆ АВС - равнобедренный, его углы при основании АВ равны по 22,5°, поэтому угол АСВ=180°-2•22,5=135°.
Угол между плоскостью ∆ АВС и плоскостью α - двугранный, и его величина равна линейному углу, образованному прямыми, лежащими в соответствующих плоскостях и перпендикулярными линия их пересечения.
ВН - высота тупоугольного ∆ АВС, проведенная к боковой стороне АС, поэтому её основание Н лежит на продолжении стороны АС.
∠ВСН - смежный ∠АСВ и равен 180°-135°=45°
ВН=ВС•sin45°=8•√2/2=4√2
ВН перпендикулярна прямой АС по построению;
наклонная КН, проведенная в точку Н, перпендикулярна прямой АС по теореме о 3-х перпендикулярах, ⇒ ∠КНВ - искомый.
Расстояние от вершины В до плоскости α равно длине перпендикуляра ВК, опущенного из точки В на плоскость α.
По условию ВК=4, ⇒sin∠КНВ=ВК:АН=4:4√2=1/√2=√2/2
Это синус 45°.
Угол между плоскостью АВС и плоскостью α равен 45°.
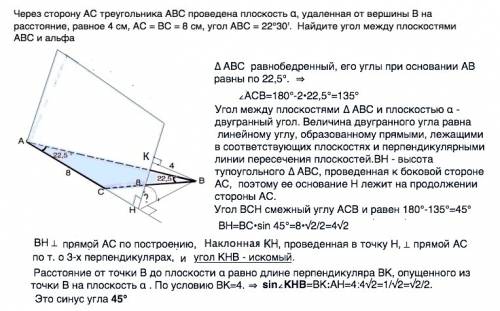
треугольник равнобедренный, поэтому углы при основании равны, угол АВС=углу ВСА=22град. 30минут. Тогда угол ВАС=180град. - 2*22град.30мин=180-45=135град
пусть расстояние от вершины В до плоскости альфа ВН=4см. Проведём перпендикуляр ВМ из вершины В на прямую АС. Треугольник тупоугольный, поэтому высота лежит за треугольником, из точки Н проведём перпендикуляр НМ на прямую АС, угол НМВ - линейный угол двугранного угла между треугольником и плоскостью альфа.
из треугольника АВМ угол ВАМ=180-135=45град. прямоугольный треугольник с углом 45 град. является равнобедренным, АМ=МВ=АВ*sin45=8* корень из2/2=4 корень из2
из прямоугольного треугольника НВМ sinHMВ=HB/MB=4/4 корень из2=1/ корень из2,
угол НМВ=45 град
Объяснение:
3 . Я думаю , що пропущено в умові задачі , що дані кути суміжні .
В такому разі маємо : нехай ∠N = x° , тоді ∠К = 3х° .
х + 3х = 180° ;
4х = 180° ;
х = 180° : 4 ;
х = 45° , тоді 3х = 3 * 45° = 135° .
В - дь : ∠N = 45° , ∠К = 135° .
4. Нехай ∠А = 45° , а зовн. ∠ACD = 130° , тоді ∠АСВ = 180°- 130°= 50° .
∠В = 180°- ( 45° + 50° ) = 85° .
Зовнішній ∠NAB = 180° - 45° = 135° .
Зовнішній ∠ABM = 180° - 85° = 95° .