Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют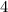 
прямых угла. (углы, градусная мера которых составляет 
).
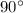Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .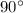
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше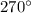 
, по условию.
Проверим: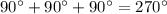 
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма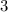 
неразвёрнутых углов составляет ровно 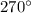, что не соответствует условию.
Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют 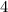прямых угла. (углы, градусная мера которых составляет ).
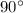Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .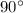
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше 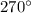, по условию.
Проверим: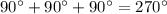
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма 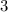неразвёрнутых углов составляет ровно 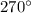, что не соответствует условию.
35°
Объяснение:
Рассмотрим треугольник ABD и DCA.
AB=CD, BD=AC - по условию, AD - общая. Треугольники равны по трём сторонам (третий признак равенства треугольников).
Из равенства треугольников следует равенство углов: <BDA=<CAD=35°