Задача: Основой прямой призмы является равнобедренный треугольник ABC, в котором АС=ВС, АВ = 6 см, ∠BAC = α, причем tgα=3/4. Найти объем призмы, если площадь ее боковой поверхности в два раза больше за площадь ее основания.
Формула объема прямой призмы:
V = S₀·h,
где S — площадь основы,
h — высота призмы
Высоту можно найти, использовав формулу боковой площади призмы:
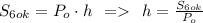 ,
,
где Po — периметр основы призмы.
Необходимо найти периметр и площадь ΔABC (основа призмы).
Рассмотрим ΔABC:
Проведем высоту CH на основу AB. Получим два прямых треугольника.
Р-м ∠ACH:
AH = AB/2 = 6/2 = 3 (см)
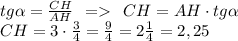
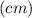
Гипотенуза AC за т. Пифагора равна:
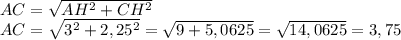
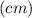
Найдем периметр ΔABC:
P = AC·2+AB = 3,75·2+6 = 7,5+6 = 13,5 (см)
Найдем площадь ΔABC:
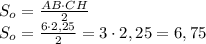
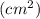
Найдем высоту призмы:
По условию, площадь боковой поверхности призмы в два раза больше площади ее основания:
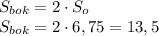
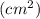
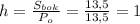
Наконец, найдем объем данной призмы:
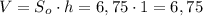
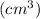
ответ: Объем призмы равен 6,75 см³.
Я беру прямоугольный треугольник со сторонами 18, 24, 30 (это "египетский" треугольник, то есть подобный известному треугольнику со сторонами 3,4,5)
От вершины прямого угла вдоль катета длины 18 я откладываю отрезок длины 10 и соединяю со вторым концом другого катета. Получился еще одни прямоугольный треугольник с катетами 10 и 24. Легко найти, что гипотенуза этого треугольника равна 26 (это Пифагорова тройка 10, 24, 26)
Если теперь посмотреть, что осталось от первоначального треугольника, если от него отрезать второй, то как раз получился треугольник со сторонами 26,18 - 10 = 8, 30. То есть - заданный в задаче.
Итак, в заданном треугольнике высота к стороне 8 равна 24. :)
Отсюда площадь равна S = 8*24/2 = 96;
ПОЛУпериметр p = (8 + 26 + 30)/2 = 32;
Радиус вписанной окружности r = S/p = 3;