∠A=∠D=74°
∠B=∠C=106°
Объяснение:
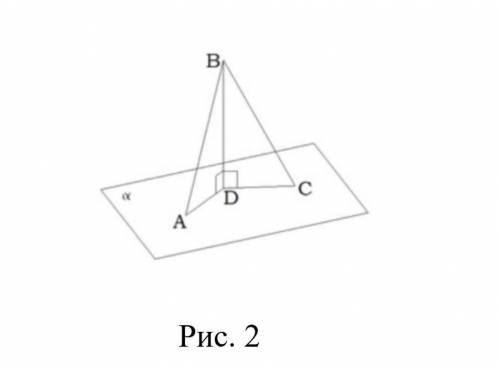
Дано: Окр.О
ABCD - вписанная трапеция.
∠АКВ=32°
О∈AD
Найти: углы трапеции.
1) ABCD - равнобедренная трапеция (вписанная)
∠АКВ=(∪AB+∪CD):2 (угол между пересекающимися хордами)
∪AB=∪CD (равными хордами стягиваются равные дуги)
32°=(∪AB+∪CD):2
2∪АВ=64° ⇒ ∪АВ=∪CD=32°
2) ∠ABD=90° (вписанный, опирается на диаметр)
∠DBC=∪CD:2=32°:2=16° (вписанный)
⇒∠B=∠ABD+∠DBC=90°+16°=106°
3) ∠A=180°-∠B=180°-106°=74° (внутренние односторонние при BC║AD и секущей АВ)
4) Углы при основаниях равнобедренной трапеции равны.
∠A=∠D=74°
∠B=∠C=106°
АD=3см
DC=3√3см
Объяснение:
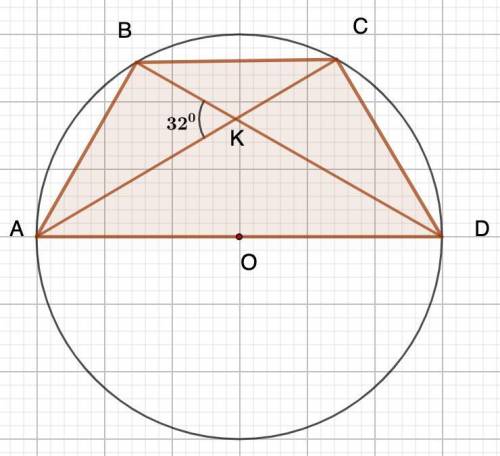
∆АВD- прямоугольный треугольник
АD- катет против угла <АВD=30°
AD=AB/2=6/2=3см
По теореме Пифагора
ВD=√(AB²-AD²)=√(6²-3²)=√(36-9)=
=√27=3√3 см.
∆СВD- прямоугольный треугольник
Углы: <ВDC=90°,по условию; <СВD=45°, по условию; <ВСD=180°-90°-45°=45°.
Углы при основании равны, ∆СВD- равнобедренный треугольник. ВD=DC=3√3см