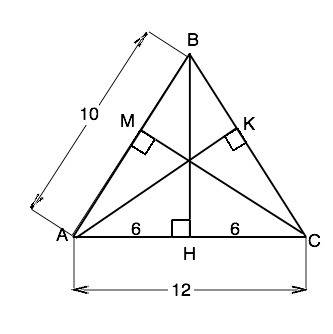
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
∆АВС ~∆А1В1С1 по двум равным углам
А=<А1, <С=<С1. Тогда сходственные стороны пропорциональны.
В ∆АВС : АС=14 , ВС= х, АВ=х-4 ;
∆А1В1С1 : А1С1=, В1С1= х-4+9, А1В1=х-4+3 .
Пропорции х:(х+5) =(х-4) :(х-1),
х-20=-х, х=10.
ВС= 10 см, АВ=10-4=6 см,
В1С1= 10-4+9=15 см, А1В1=10-4+3=9 см.