
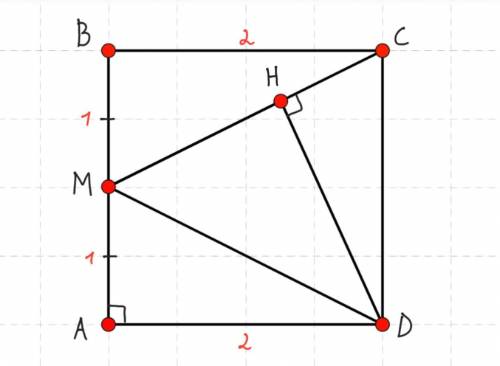
Дано: ABCD — квадрат, Sabcd= 4, т.М — середина АВ, АМ=ВМ, DH⟂СМ.
Найти: DH.
Решение.
1) Найдем сторону квадрата.
АВ²= 4;
АВ= 2 (–2 не подходит).
AB=BC=CD=AD= 2.
т.M — середина АВ, значит, АМ=ВМ= 2:2= 1.
2) Мы видим два равных прямоугольных треугольника: ΔMBC и ΔMAD (равны по двум катетам).
Найдем их площадь. Площадь прямоугольного треугольника равна половине произведения его катетов.
Значит, Smbc= Smad= ½•1•2= 1.
3) А площадь треугольника MDC равна разности площади квадрата и площадей треугольников MBC и MAD.
Т.е. Smdc= Sabcd–Smbc–Smad= 4–1–1= 4–2= 2.
4) Найдем сторону МС прямоугольного треугольника МВС (МС - это гипотенуза) по т.Пифагора:
МС²= МВ²+ВС²;
МС²= 1+2²;
МС²= 5;
МС= √5
5) Площадь обычного (произвольного) треугольника равна произведению половины основания этого треугольника на высоту, проведённую к этому основанию.
Для треугольника MDC это выглядит так:
Smdc= ½•MC•DH.
2= ½•√5•DH;
2 : ½ = √5DH;
√5DH= 4;
DH= 4/√5.
Расстояние от вершины D квадрата ABCD до прямой СМ равно 4/√5.
ОТВЕТ: 4/√5.
Объяснение:
Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него треугольник, подобный данному.
1. MN || BC => △AMN~ △AВС => MN/BC=AM/AB; AM=MN*AB/BC=5*18/15=6
2. PD || AC => △PBD~ △AВС => PD/AC=BD/BC; BC=AC*BD/PD=9*4/3=12
3. DE || AB => △ECD~ △BCA => CE/CB=DE/AB; CB=CE+BE=6+2=8; AB=CB*DE/CE=8*4/6=5 1/3 (пять целых одна третья)
4. MN || AC => △ABC~ △MBN => AC/MN=BC/BN;
AC/MN=5/12; BN=BC+CN=BC+8;
5/12=BC/(BC+8)
12BC=5(BC+8)
12BC=5BC+40
7BC=40
BC=40/7=5 5/7 (пять целых, пять седьмых)