подобен
подобен  , тогда
, тогда 
1200√3 см²
Объяснение:
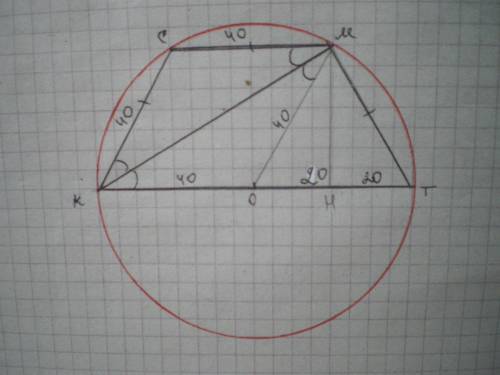
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°, КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).
∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.
∠СКМ=∠ТКМ за умовою, ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.
Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною, отже КС=СМ=КО=ОМ=40 см.
МТ=КС=40 см.
ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.
ОН=ТН=40:2=20 см
За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.
S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²
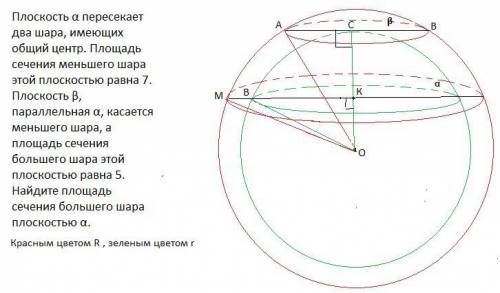
Плоскость α пересекает два шара, имеющих общий центр. Площадь сечения меньшего шара этой плоскостью равна 7. Плоскость β, параллельная α, касается меньшего шара, а площадь сечения большего шара этой плоскостью равна 5.(бедные дети) Найдите площадь сечения большего шара плоскостью α.
Объяснение:
Рассмотрим сечение данной комбинации тел и плоскостей , проходящее через диаметры шаров и перпендикулярно секущим плоскостям α и β. Пусть радиусы большого шара R ,малого шара r.
S(кр)=πr² , S(крАС)=5 ⇒ АС=√5/π, S(крКВ)=7 ⇒ КВ=√7/π.
В сечении большего шара плоскостью α получаем круг с радиусом КМ , S(КМ)= π* КМ² .
ΔМКО-прямоугольный , R²= КМ²+КО² (1)
ΔВКО-прямоугольный , r²= КВ²+КО² (2). Вычтем из (1) уравнения (2).
R²-r²=КМ²-КВ² (3).
ΔАСО-прямоугольный , ОА²=СО²+АС² или R²=r²+АС² или
R²- r²= АС² подставим в (3).
АС²=КМ²-КВ² или КМ²=АС²+КВ²
КМ²=(√5/π)²+(√7/π)²=12/π
S(КМ)= π* КМ²=π*12/π=12 (ед²).