Дано:
∆ ABC,
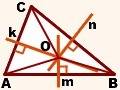
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
Доказательство:
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
Найти медиану AM треугольника ABC, вершинами в точках: A(-2: 0), B(0; 5), C(4; 1).
Находим координаты точки М как середины стороны ВС.
М = (B(0; 5) + C(4; 1))/2 = (2; 3).
Теперь находим длину медианы АМ:
АМ = √((2-(-2))² + (3-0)²) = √(16 + 9) = √25 = 5.
ответ: АМ = 5 ед.