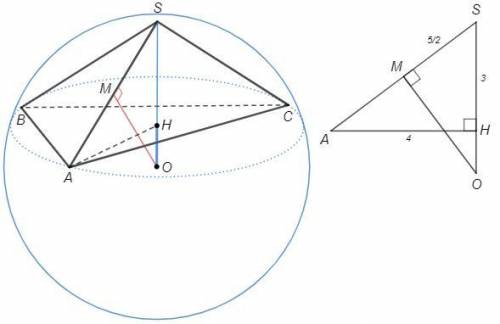
Основание ABC, AB=4, ∠C=30°
H - центр описанной окружности.
AB/sinC =2AH (т синусов) => AH=4
Если боковые ребра пирамиды равны, то вершина падает в центр описанной окружности основания.
SH⊥(ABC)
SH=√(SA^2-AH^2) =3 (т Пифагора)
О - центр описанной сферы.
OABC - пирамида с равными боковыми ребрами, следовательно ее вершина также падает в центр H.
OH⊥(ABC)
S-H-O на одной прямой.
В плоскости ASO.
OS=OA, О на серединном перпендикуляре к SA.
M - середина SA, SM=5/2
△SOM~△SAH
SO/SA=SM/SH => SO/5=5/2*3 => SO=25/6
OH =SO-SH =25/6 -3 =7/6
a) <A=60, <B=40, c=14
БС=180-40-60=80
AB/SinC=BC/SinA=AC/SinB
14/Sin80=BC/Sin60=AC/Sin40
14/0.9848=BC/0.8660=AC/0.6428
14/0.9848=BC/0.8660 => BC=14*0.8660/0.9848=12.3
14/0.9848=AC/0.6428 => AC=14*0.6828/0.9848=9.1
б) a=6.3, b=6.3, <C=54
c^2=a^2+b^2-2*a*b*CosC=6.3^2+6.3^2-2*6.3*6.3*Cos54=39.69+39.69-79.38*0.5878= 79.38-46.659564=32.720436=5.7
a=b =6.3 => <A=<B=(180-54)/2=126/2=63
Объяснение:
всё легко