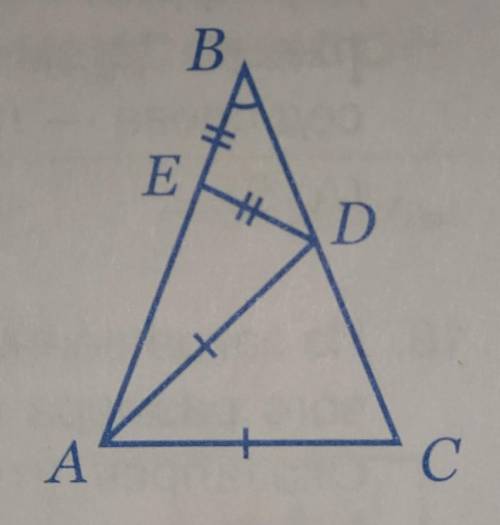
Сначала найдем высоту BD, из прямоугольного ΔBCD по теореме Пифагора
BD² = BC² - CD² = 37 - 5² = 37 - 25 = 12,
BD = √(12) = 2*√3 см.
Из прямоугольного ΔABD найдем:
∠ABD = 180° - 90° - ∠BAD = 90° - 30° = 60°.
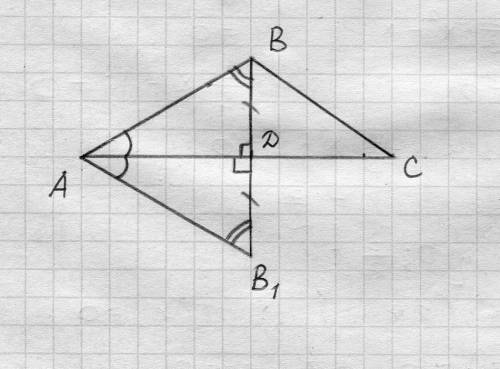
Продолжим отрезок BD за точку D и отложим на прямой BD отрезок
DB₁ = BD. И проведём отрезок AB₁. Тогда прямоугольный
ΔABD = ΔAB₁D (по двум катетам и прямому углу).
Тогда ∠AB₁D = ∠ABD = 60° и тогда 30° = ∠A = ∠BAD = ∠B₁AD, и
∠BAB₁ = ∠BAD + ∠B₁AD = 30° + 30° = 60°
Получаем, что в ΔBAB₁ все углы по 60°. Против равных углов в треугольнике лежат равные стороны, поэтому ΔBAB₁ равносторонний, поэтому AB = BB₁,
BB₁ = BD+DB₁ = 2*BD = 2*2*√3 = 4*√3 и
AB = BB₁ = 4*√3.
Из прямоугольного ΔABD по теореме Пифагора найдем AD:
AD² = AB² - BD² = (4*√3)² - (2*√3)² = 16*3 - 4*3 = 12*3 = 36,
AD = √36 = 6 см.
AC = AD+CD = 6см+5см = 11см.
S(ΔABC) = (1/2)*AC*BD = (1/2)*(11см)*(2*√3 см) = 11*√3 см²
1. Сумма углов в любом треугольнике равна 180°. Найдем угол A: 180 - ( 56 + 64 ) = 60°.
BC = 3√3 ( по условию ), противолежащий угол A = 60°.
По теореме синусов:
(3√3) / sin 60° = 2R
(3√3) / (√3/2) = 2R
6 = 2R
R = 3.
2. В равнобедренном треугольнике углы при основании равны. Найдем углы при основании треугольника ABC: (180 - 36) / 2 = 72°.
Значит угол BAC = BCA = 72°.
AD - биссектриса, делит угол BAC на два равных угла: BAD = DAC = 36°.
В треугольнике ADC нам известны два угла: DAC = 36°, DCA = 72°. Найдем третий угол:
180 - ( 72 + 36 ) = 72. Значит треугольник ADC - равнобедренный, так как углы при его основании равны.
75°
Объяснение:
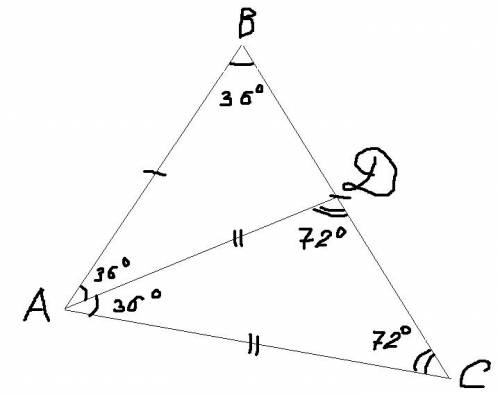
В равнобедренном треугольнике углы при основании равны.Сумма углов треугольника равна 180°.1) ΔАВС: ∠ВАС=∠С=(180°-∠В)÷2=(180°-30°)÷2=75°
2)ΔADC: ∠ADC=∠C=75°
3)ΔВЕD: ∠EDB=∠B=30°
∠BDC - развёрнутый угол его градусная мера 180°
∠EDA=180°-∠EBD-∠C=180°-30°-75°=75°