1.Углы альфа и бетта вписанные, значит они равны половине дуги на которую опираются, следовательно дуга соответствующая углу альфа равна 21*2=42(град), а дуга соответствующая углу бетта 49*2=98(град).
Найдем градусную меру дуги соответствующую углу х, 360-(180+98+42)=40, значит угол х=1/2*40=20(град)
ответ: 20град.
2.2х+3х+4х=180
9х=180
х=20
20*2=40(1-ый угол)
20*3=60(2-ой угол)
20*4=80(3-ий угол)
Проверка:
40+60+80=180
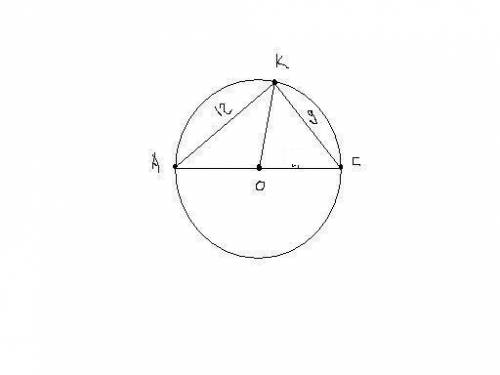
3.В треугольнике АКС угол К-прямой=90 градусов. Т.к Хорды окружности АК и КС построены из одной точки К на концы диаметра. Отсюда по тореме пифагора АС²=АК²+КС²
АС²=12²+9²=225
АС=√225=15
Радиус равен 15/2=7,5 (рисунок внизу)
Высота, опущенная из вершины прямого угла на гипотенузу, делит прямоугольный треугольник на подобные треугольники.
Гипотенуза прямоугольного треугольника равна длине двух его медиан.
Пусть коэффициент данного по условию отношения высоты и медианы будет 1.
Тогда высота равна 40, медиана 41, гипотенуза 2*41=82
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Примем отрезок АН гипотенузы за х, НВ тогда 82-х
Квадрат высоты равен произведению отрезков АН и НВ
СН²=АН*НВ
1600=х(82-х)
х²-82х+1600=0
Решив квадратное уравнение, найдем два значения х=50 и х=32.
АН, как более короткий отрезок, равен 32,
НВ=50
Треугольники АНС, СНВ и АВС подобны .
И отношение их катетов одинаково.
Найдем отношение известных катетов в треугольниках АНС и СНВ. АН:СН=СН:НВ=4:5
АС:СВ=4/5
Но всегда простое решение - лучше сложного.
Вариант решения:
Основа решения:
Гипотенуза прямоугольного треугольника равна длине двух его медиан.
Между медианой и высотой образовался прямоугольный треугольник с гипотенузой СМ=41 и катетом СН=40.
По т.Пифагора отрезок гипотенузы НМ=9.
И тогда катет АН треугольника АНС относится к соответственному катету СН подобного ему треугольника СНВ как АН:НС=32:40=4/5
И вариант третий - если знать, что в треугольнике с гипотенузой 41, и катетом 40 второй катет равен 9 ( одна из троек Пифагора)- позволяет обойтись самым минимумом вычислений.
1. Рисуем плоскости (в виде полуприкрытой книги).
В верхней плоскости выбираем точку А и опускаем из неё перпендикуляр АС на нижнюю плоскость. АС=6 см.
Из точки А проводим перпендикуляр АВ к линии пересечения плоскостей.
АВ=12 см.
Получаем прямоугольный треугольник АВС с прямым углом С.
Находим угол В через его синус: sinB=AC:AB
sinB=6:12=1/2
B=30 град - это и есть угол между плоскостями.
2.
Даны точки М(3;0;-1), К(1;3;0), Р(4;-1;2). Найдите на оси Ох такую точку А, чтобы векторы МК и РА были перпендикулярны.
вектор МК(1-3;3-0;0+1)=(-2;3;1)
вектор РА(4-х;-1-у; 2-z)
A принадлежит оси ОХ, начит её координаты равны А(х;0;0)
вектор РА(4-х;-1-0; 2-0)=(4-х; -1;2)
векторы перпендикуляны, когда их произведение равно 0.
МК*РА=-2(4-х)+3(-1)+1*2=0
-2(4-х)-3+2=0
-8+2х-1=0
2х=9
х=4,5
А(4,5;0;0) - искомая точка
3. Можно воспользоваться рисунком из первой задачи, причём в верхней плоскости изобразить равносторонний треугольник АВС, основание которого АВ лежит на линии пересечения плоскостей.
1)Из вершины С опускаем два перпендикуляра, один СН на нижнюю плоскость, а второй СF - к линии пересечения плоскостей.
2)Треугольник АВС-равносторонний (по условию), АВ=ВС=АС=m
Высота AF треугольника АВС равна sqr(m^2-(m/2)^2)=msqr(3)/2
3)Теперь найдём расстояние от третьей вершины треугольника до плоскости альфа: АН=sin фи * msqr(3)/2