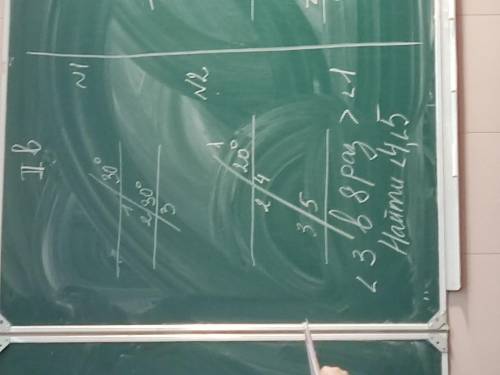
ответ:
сумма углов, примыкающих к стороне, равна 180 градусам, поэтому сумма их половин, отсекаемых биссектрисами, равна 90 градусам. отсюда следует, что efgh -- прямоугольник, и сумма квадратов его сторон равна удвоенному квадрату диагонали.
пусть e -- точка пересечения биссектрис углов a и d. середина k стороны ad равноудалена от вершин прямоугольного треугольника ade. при этом угол ked равен kde, а также cde, поэтому ke параллельна cd и является частью средней линии kl параллелограмма. на этой же линии лежит и точка g из аналогичных соображений.
таким образом, eg=kl−ke−gl=ab−1\2ad−1\2bc=ab−ad=3\2 есть длина диагонали. следовательно, в ответе получится 2(3\2)2=9\2.
объяснение:
Дуга равна соответственному центральному углу.
∪CA = 360°−∪AB−∪BC = 360−96−106 = 158°
I — центр вписанной окружности в треугольник; IA = IB = IC — радиусы.
∢AIC = ∪CA = 158°; ∢AIB = ∪AB = 96°; ∢BIC = ∪BC = 106°
IA ⊥ LM, IB ⊥ MN, IC ⊥ NL (радиус ⊥ к касательной)
∢IAM = ∢MBI = ∢IBN = ∢NCI = ∢ICL = ∢LAI = 90°
∢L= 360°−∢AIC−∢LAI−∢ICL = 360−158−90−90 = 360−180−158 =180(2-1)-158=180-158 = 22° (из 4-угольника AICL)
аналогично для других углов:
∢ M= 180−96 = 84°
∢ N= 180−106 = 74°
∢L= 22°∢M = 84°∢N = 74°∪CA = 158°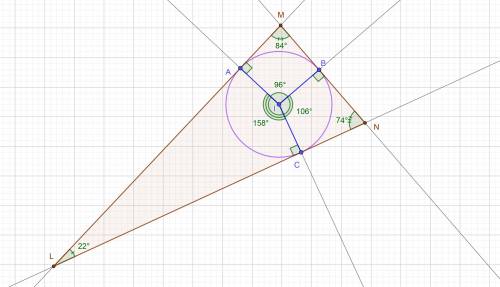
Номер 1
Можно даже не вычислять,чему равны углы 1;2;3;
Два угла 30 градусов называются соответственными,если при пересечении двух прямых секущей соответственные углы равны,то прямые параллельны
<1=<30=30 градусов,как накрест лежащие,вообще-то-смотрятс каким из двух углом сравнивать
<1+<2=180 градусов,как односторонние
<2=180-30=150 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<3=<2=150 градусов,как вертикальные
Номер 2
<20=<2=<20 градусов,как вертикальные
Если угол 3 в 8 раз больше угла 2,то
<3=20•8=160 градусов
<3=20+160=180 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<4=<3=160 градусов,как накрест лежащие
<5=<2=20 градусов
Объяснение: