построем рисунок, в треугольнике ВСD: ВС=СD (т.к. шестиугольник правильный), угол равен 120 градусов, (по формуле для нахлждения угла в правильном многоугольнике а=180(n-2)/n), проведһм перпендикуляр СН, угол ВHC = (180-120)/2=30 (т.к. треугольник равнобедренный, углы при основании равны) следовательно, СН=0,5ВС = корень из 48 по полам=корень из двенадцати (после преобразования)
теперь ВН = (по теореме пифагора) корень из (48-12) = корень из 36 = 6
ВН равно HD (т.к. в равнобедренном треугольнике высота равна медиане) следовательно ВD=2BH = 6*2 = 12
Как то так!
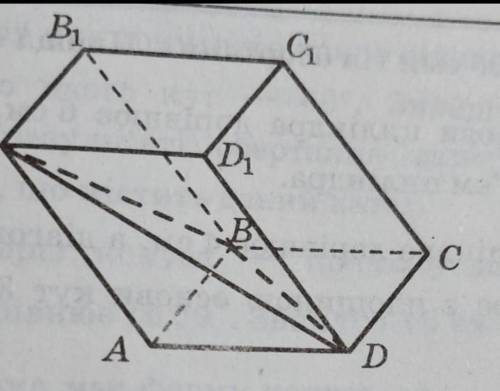
Параллелепипед ABCDA1B1C1D1 и пирамида ABDA1 имеют общую высоту - это перпендикуляр H, опущенный из общей вершины A1 на плоскость ABC.
Из формулы объёма пирамиды V = (1/3)SoH выразим Н.
H = 3V/So. Здесь So – площадь треугольника АВD.
У параллелепипеда площадь S основания в 2 раза больше.
То есть: S = S(ABCD) = 2So.
Объём параллелепипеда Vп = SH = 2So*(3V/So) = 6V.
ответ: объём параллелепипеда Vп = 6V.