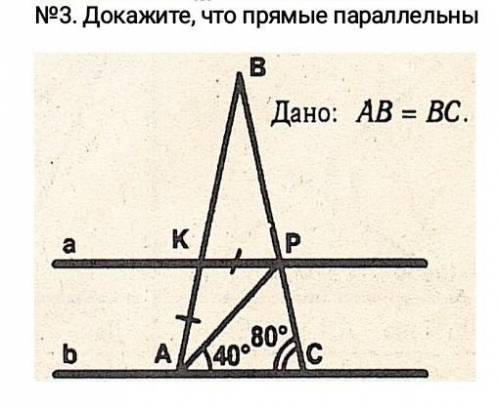
<ВАС=<ВСА=80 градусов, т. к АВ=ВС, тр-к АВС-равнобедренный
<КАС=<РСА=<ВАС=80 градусов,
<КАР=<АРК=<КАС-<РАС=80-40=40 градусов,
<АКР=180-2×<КАР=180-2×40=100 градусов,т.к
тр-к АКР - равнобедренный (АК=КР)
Сумма односторонних углов равна 180 градусов :
<АКР+<КАС=100+80=180 градусов,
значит прямые а и b параллельны
такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
ответ:Если по условию задачи АВ=ВС,то треугольник АВС равнобедренный,а значит,что углы при основании равны между собой
<ВАС=<С=80 градусов
Тогда
<КАР=80-40=40 градусов
Треугольник АКР равнобедренный по условию задачи,значит
<КАР=<АРК=40 градусов
<АКР=180-40•2=100 градусов
Треугольник АРС
<АРС=180-(40+80)=60 градусов
<КРС=40+60=100 градусов
Четырёхугольник АКРС на самом деле равнобокая трапеция,т к углы при каждом основании равны между собой
Мы можем утверждать,что прямые параллельны хотя бы потому,что по определению основания трапеции параллельны,т е
КР || АС
Но ещё и равны накрест лежащие углы
<РАС=<АРК=40 градусов,как накрест лежащие при КР || АС и секущей АР
Объяснение: