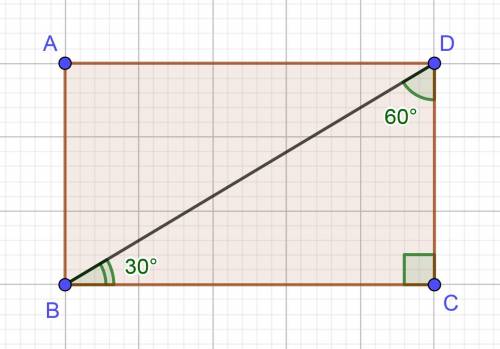
Нехай дано прямокутник ABCD, BD — діагональ, DC = 10 см, ∠BDC = 60°.
Р-мо BDC:
∠BCD = 90° — як кут прямокутника, отже ΔBDC — прямий, ∠BDC = 60° — за умовою, тоді ∠DBC за теоремою про суму кутів трикутника буде дорівнювати:
∠DBC = 180°−90°−60° = 30°.
По властивості катета, який лежить напроти кута 30°, гіпотенуза трикутника буде рівна:
BD = 2*DC = 2*10 = 20 (cm)
Знайдемо інший катет за т. Піфагора:
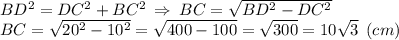
Підставимо значення у формулу площі прямокутника:

Відповідь: Площа прямокутника рівна 100√3 см² або приблизно 173,2 см².
13:10:9
Объяснение:
Угол А=3x
Угол B=6x
Угол С=7x
Поскольку внешний угол треугольника
равен сумме 2-х внутренних, не смежных
с ним то:
УголCBN=уголA+уголC=10x
<BCL=<A+<B=9x
<CAP=2B+<C=13x
Отношение:13:10:9