Часть круга, расположенная вне ромба - это два равных сегмента круга, отсекаемых от него ромбом.
Формула площади сегмента круга
S=0,5•R*•[(π•a/180)-sinα, где α - угол сегмента.
Диагонали ромба пересекаются под прямым углом.
Катет прямоугольного треугольника - среднее пропорциональное между гипотенузой и проекцией этого катета на неё.
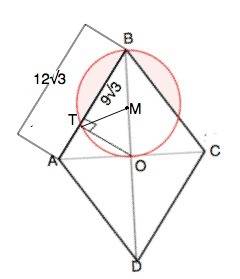
Из ∆ АОВ диаметр ВО=√АВ•BТ=√12√3•9√3=18 см.
ТM=BM=OM=R=9
Высота прямоугольного треугольника, проведенная из прямого угла - среднее пропорциональное между отрезками, на которые она делит гипотенузу.
ОТ=√AT•BT
AТ=12√3-9√3=3√3
ОТ=√3√3•9√3=9
ОТ=9⇒ОТ= R⇒
∆ТMO-равносторонний,∠ТМО=60° ⇒ смежный ему∠ТМВ=120°
2S=81•[(π•120°/180°)-√3:2], откуда после вычислений получаем 2S=13,5•(4π-3√3) или ≈99,5 см²
В треугольнике ABC ∠С = 90°, AB = 5, tgA = 7/24. Найдите AC.
===========================================================
▪Первый теорема Пифагора ):tgA = BC/AC = 7/24Пусть ВС = 7х, АС = 24х, тогда Применим теорему Пифагора:АС² + ВС² = АВ²( 24х )² + ( 7х )² = 5²576х² + 49х² = 25625х² = 25х² = 1/25 ⇒ х = 1/5 = 0,2 Значит, АС = 24х = 24•0,2 = 4,8▪Второй Тригонометрия ):tg²A + 1 = 1/cos²Acos²A = 1/( tg²A + 1 ) = 1/( (7/24)² + 1 ) = 1/( 625/576 ) = 576/625cosA = ± 24/25 ⇒ ∠A - острый ⇒ cosA = 24/25cosA = AC/AB = 24/25 ⇒ AC = ( 5 • 24 )/25 = 24/5 = 4,8ОТВЕТ: 4,8