
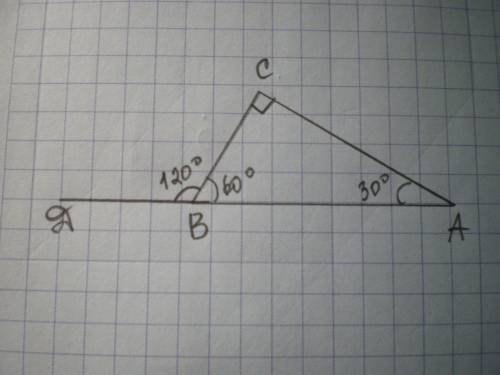
Дано: ΔАВС - прямоугольный, ∠С=90°, ∠ДВС=120°, АВ+ВС=24 см.
Найти АВ, ВС.
По свойству смежных углов ∠ДВА+∠СВА=180°, тогда
∠СВА=180-∠ДВС=180-120=60°.
По свойству острых углов прямоугольного треугольника
∠А=90-∠СВА=90-69=30°
В треугольнике против большей стороны лежит больший угол, поэтому АВ - большая сторона. Против меньшей стороны лежит меньший угол, поэтому ВС - меньшая сторона.
ВС=1\2 АВ по свойству катета, лежащего против угла 30°.
Составим уравнение: АВ+1\2 АВ = 24; 1,5 АВ = 24; АВ=16 см.
ВС=16:2=8 см.
ответ: 8 см, 16 см.
Пирамида SАВСД: основание АВСД (АВ=ВС=СД=АД=12). Вершина пирамиды S проектируется в точку О пересечения диагоналей основания (квадрата) АС и ВД, т.е. SO - это высота пирамиды.
Проведем апофему пирамиды SK - это высота боковой грани.
Двугранный угол SKО равен 30°.
Из прямоугольного ΔSKО найдем SK (KO=АВ/2=12/2=6):
SK=ОК/cos 30=6 / √3/2=12/√3=4√3
Площадь основания Sосн=АВ²=12²=144
Периметр основания Р=4АВ=4*12=48
Площадь боковой поверхности
Sбок=P*SK/2=48*4√3/2=96√3≈166,28
Площадь полной поверхности
Sполн=Sбок+Sосн=96√3+144≈310,28