Сумма углов треугольника равна 180°. Так как углы при основании равнобедренного треугольника равны, то угол при вершине равен 180° - 2*30° = 180 - 60 = 120°.
Площадь треугольника равна:
S = 0.5 * AB * BC * sinB = 0.5 AB²sin120°, где AB = BC как боковые стороны.
Тогда AB² = 2S/sin120° = 2*4√3/(√3/2) = 16 ⇒ AB = 4
Теперь рассмотрим прямоугольный треугольник, который образован искомой высотой, одной из боковой сторон и половиной длины основания. Угол, противолежащий искомой высоте, равен 30° по условию. Тогда, по определению синуса, h = AB*sin30° = 4 * 0.5 = 2.
ответ: 2
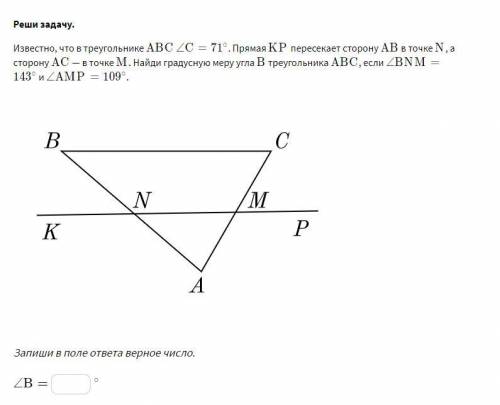
∠В = 37°
Объяснение:
∠NMC =∠AMP = 109° - как вертикальные.
∠NMC и ∠С - внутренние односторонние углы, образованные при пересечении прямых ВС и КР секущей АС.
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.Проверяем: ∠NMC + ∠С = 109° + 71° = 180°, ⇒ ВС ║ КР.
∠ВNM и ∠В - внутренние односторонние углы, образованные при пересечении параллельных прямых ВС и КР секущей АВ. Так как их сумма равна 180º, то:
∠В = 180° - ∠ВNM = 180° - 143° = 37°