Question

Отрезки AC и BD делятся точкой О пополам. Докажи, что AB || CD.

Answer 1

Итак, 1)ΔAOC=ΔBOD по двум сторонам и углу между ними( AO=OB, CO=OD, ∠AOC=∠BOD как вертикальные) Из равенства следует, что ∠CAB=∠ABD, но они накрест лежащие при пересечении прямых AC и BD секущей AB, значит эти прямые параллельные.
Доказано)

Answer 2

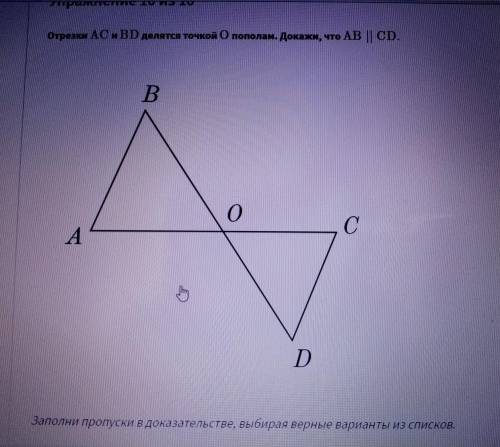
Рассмотрим треугольники АВО и ОСД:

углы ВОА и СОД равны тк вертикальные,

ВО=ОД и АО=ОС по условию задачи

Следовательно треугольники равны по двум сторонам и углу между ними

Следовательно углы ОВА и ОДС равны

тк углы ОВА и ОДС равны, ВД - секущая для прямых АВ и ДС, следовательно АВ паралельна СД, тк эти углы являются накрест лежащие при секущей, пересекающей две параллельные прямые

ЧТД

Answer 3

Для доказательства того, что отрезки AB и CD параллельны, мы можем использовать свойство перпендикулярных диагоналей параллелограмма.

Дано: отрезки AC и BD делятся точкой О пополам.

Перспективный план доказательства:
1. Покажем, что треугольники ADO и CBO равны.
2. Из равенства треугольников следует, что их соответствующие стороны пропорциональны.
3. Это означает, что отношение AD/BC равно отношению AO/CO.
4. Так как AO = CO (точка O делит отрезки AC и BD пополам), то и AD = BC.
5. По свойству перпендикулярных диагоналей параллелограмма следует, что AB || CD.

Шаг 1: Докажем, что треугольники ADO и CBO равны.
Мы знаем, что точка О делит отрезки AC и BD пополам, поэтому AO = OC и BO = OD.
Также, по условию, отрезки AD и CB пересекаются в точке О.
Теперь рассмотрим треугольники ADO и CBO:
- У них есть общий угол O.
- У них есть равные противоположные углы, так как AO = OC (точка О делит отрезки AC и BD пополам).
- У них есть равные гипотенузы AO и OC.
Таким образом, треугольники ADO и CBO равны по двум сторонам и углу, что по теореме равных треугольников означает их полное равенство.

Шаг 2: Из равенства треугольников следует, что их соответствующие стороны пропорциональны.
Из равенства треугольников ADO и CBO следует, что соответствующие стороны пропорциональны:
AD/CO = AO/CO.

Шаг 3: Отношение AD/BC равно отношению AO/CO.
Из шага 2 мы знаем, что AD/CO = AO/CO.
Перегруппируем это равенство, чтобы получить:
AD/BC = AO/CO.

Шаг 4: AD = BC.
Так как AO = CO (точка О делит отрезки AC и BD пополам), то отношение AO/CO равно 1.
Подставим это в равенство из шага 3:
AD/BC = 1.
Умножим обе части на BC:
AD = BC.

Шаг 5: AB || CD.
Мы знаем, что отрезки AD и CB пересекаются в точке О.
Также, мы доказали, что AD = BC.
Следовательно, отрезки AB и CD, которые являются продолжениями отрезков AD и BC, одного и того же отрезка, параллельны друг другу.

Таким образом, мы доказали, что отрезки AB и CD параллельны, основываясь на свойстве перпендикулярных диагоналей параллелограмма и равенстве треугольников ADO и CBO.