Так как в параллелограмме противолежащие стороны попарно параллельны и равны, то в параллелограмме MKPT MK=PT и KP=MT
Так как KP=MT, то диагональ MP является секущей, которая пересекает две параллельные прямые, тогда:
∠PMT = ∠KPM как накрест лежащие углы.
Так как МР является бисектрисой ∠M, то:
∠KMP = ∠PMT
Таким образом у нас получается :
∠PMT = ∠KPM = ∠KMP
В △MKP ∠KPM = ∠KMP, таким образом △MKP равнобедренный, тогда: МК=КР=Х
Так как MK = PT, то PT = KP = x, а также KP = MT = x.
В паралекграмме МКРТ все стороны равны х. Его периметр тогда будет равнятся:
P = MK + KP + PT + MT = x + x + x + x = 4×х
Теперь решаем:
4×х=60
х=60÷4
х=15
ответ: каждая сторона параллеграмма равна 15 см
32,475 ед²
Объяснение:
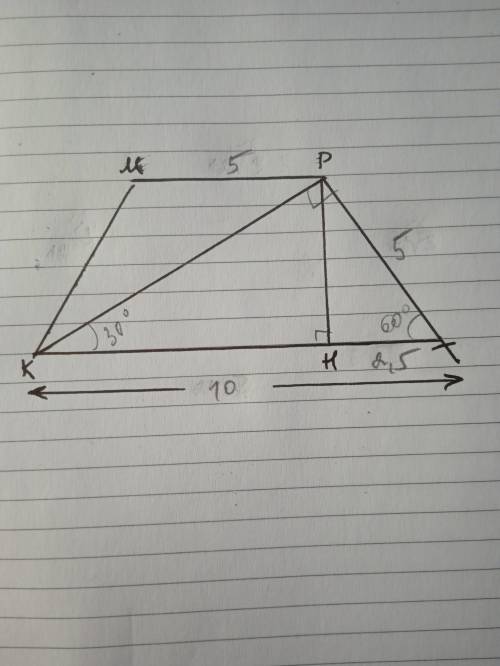
Дано: КМРТ - трапеция, КМ=РТ, КТ=10; ∠К=∠Т=60°. КР⊥РТ Найти S(КМРТ).
ΔКРТ - прямоугольный, ∠Т=60°, ∠РКТ=90-60=30°, т.к. сумма острых углов прямоугольного треугольника 90°
РТ=1\2 КТ=10:2=5 по свойству катета, лежащего против угла 30°
Проведем высоты МС и РН, рассмотрим ΔТРН - прямоугольный,
∠ТРН=90-60=30°, значит ТН=1/2 РТ=5:2=2,5.
По теореме Пифагора РН=√(РТ²-ТН²)=√(25-6,25)=√18,75≈4,33
ΔКМС=ΔТРН по катету и гипотенузе, значит КС=ТН=2,5;
МР=СН=10-2,5-2,5=5.
S=(МР+КТ):2*РН=(5+10):2*4,33≈32,475 ед²