Вот если провести через ЭТУ вершину тупого угла прямую перпендикулярно МЕНЬШЕЙ диагонали, а ТУ САМУЮ сторону, к которой проведена (из ЭТОЙ вершины) высота, продлить до пересечения с этим перпендикуляром, то получится прямоугольный треугольник, у которого катеты равны диагоналям ромба, а высота к гипотенузе делит их на отрезки n и m + (m + n) = n + 2*m; (сама гипотенуза равна 2*(m + n)) Отсюда высота к гипотенузе определяется так h^2 = n*(n + 2*m); и меньшая диагональ ромба (которая соединяет вершины тупых углов) n^2 + h^2 = d^2 = 2*n^2 + 2*m*n = (m + n)^2 + n^2 - m^2; Большая диагональ D^2 = 4*(m + n)^2 - d^2 =3*(m + n)^2 + m^2 - n^2;
Высота проведена к большему основанию. У нас получился прямоугольный треугольник, две стороны нам известны, находим третью по теореме Пифагора: 5²-4²=х² х²=25-16=9 х=3 Проводим высоту из второй вершины к этому же основанию.У нас получается два прямоугольных треугольника. Так трапеция равнобедренная, то гипотенузы равны Высоты одной трапеции равны, следовательно, у нас есть равные катеты Треугольники равны по гипотенузе и катету, значит, неизвестная сторона второго треугольника тоже равна 3 После проведения двух высот у нас получился квадрат, сторона которого равна меньшему основанию.Находим её: 10-3-3=4 Средняя линия равна полусумме оснований: (10+4)/2=7 Площадь трапеции равна полусумме оснований на высоту (10+4)/2 х4=28
Пусть стороны равны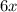
и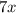 
. Тогда площадь:
Отрицательный корень не подходит, т.к. длина — величина положительная: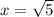
.
Тогда стороны равны:
Проверка:
Отношение сторон:
Площадь:
Всё верно.
Появились вопросы? Задавай, с радостью объясню.