1)углы при основании трапеции не могут быть 450 и 300. Это ловушка х). 450 - 360 = 90 градусов один угол, значит трапеция прямоугольная , следовательно, если высота равна 6 , то и одна боковая сторона равна 6.
2) 2-ой угол = 300 - 180 = 120, а сумма углов трапеции при одной боковой стороне равна 180 градусов ,то второй угол равен 180 -120 = 60
3) проведя высоту в трапеции, мы получим прямоугольный треугольник с катетом 6 см и углом 60 градусов , значит другой угол в этом треугольнике равен 90 - 60 = 30, а катет лежащи против угла в 30 градусов равен половине гипотенузы, но этот катет неизвестен, тогда обозначим его через x , тогда гипотенуза = 2x . По теореме Пифагора: 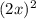 =
=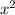 +6
+6
4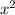 -
-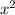 =6
=6
3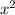 =6
=6
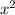 =2
=2
x = 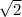 (отрицательное значение не берём)
(отрицательное значение не берём)
Рассмотрим треугольники ANC и AMC:
У них есть общее основание - АС, и равные углы при основании, т.к. углы при основании в равнобедренном треугольнике равны. Имеем: угол NAC = углу MCA по условию задачи, но углы BAC=BCA, то есть равны и другие части этих углов - угол МАN=NCM. Таким образом треуг.AMC=треуг.ANC по стороне и двум углам.
В равных треугольниках против равных углов лежат равные стороны. Следовательно, AM=NC. Так как треуг.ABC - равнобедренный, то MB=NC, (AB-AM =MB) = (BC-NC=BN), где AB=BC AM=NC.
То есть треугольник MBN - равнобедренный ч.т.д