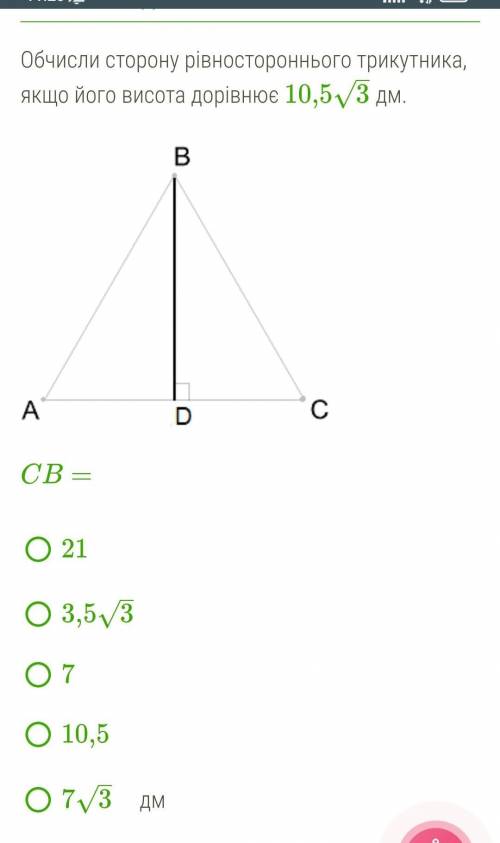
15°, 150° и 15°
Объяснение:
Треугольник ABN - равносторонний, т.е. AB=AN=BN
Но ABCD - квадрат => AB=AN=BN=BC=CD=AD
Рассмотрим треугольник ADN:
<A=90°-<BAN = 90°-60° =30°
AD=AN => треугольник ADN - равносторонний
Значит, <ADN=<AND=(180°-30°)/2 = 75°
Рассмотрим треугольник BCN:
<B=90°-<ABN = 90°-60° =30°
BC=BN => треугольник BCN - равносторонний
Значит, <BNC=<BCN=(180°-30°)/2 = 75°
Рассмотрим треугольник DNC:
<CDN = 90°-<ADN = 90°-75° = 15°
<DCN = 90°-<BCN = 90°-75° = 15°
<DNC = 360° -<AND-<ANB-<BNC = 360°-75°-60°-75° = 150°


6 ед.
Объяснение:
В правильной усеченной пирамиде в основаниях лежат правильные многоугольники, стороны которых соответственно равны между собой. Боковые грани такой пирамиды - равные между собой равнобокие трапеции. Радиусы окружностей, вписанных в основания, проведенные в точки касания сторон оснований с соответственной окружностью Н и Н1, перпендикулярны к сторонам оснований по свойству радиусов, проведенных в точки касания.
Проведем перпендикуляр из точки касания Н1М верхнего основания на нижнее основание. Тогда отрезок Н1Н перпендикулярен стороне основания АВ по теореме о трех перпендикулярах, то есть является искомой высотой боковой грани.
В прямоугольном треугольнике НН1М угол ∠НН1М = 30° по сумме острых углов. Следовательно, НН1 = 2·НМ по свойству катета, лежащего против угла 30°.
НМ = ОН - О1Н1 = 8-5 = 3 ед.
Высота боковой грани НН1 = 6 ед.