
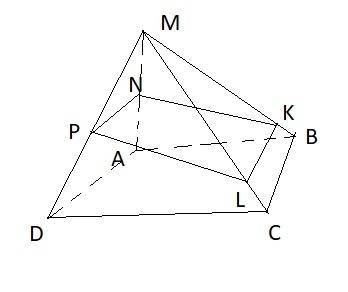
Для построения заданного сечения соединим точки N и K.
Т.к. сечение параллельно AD и проходит через точку N, то проводим в плоскости MAD прямую NP, параллельную AD - это средняя линия треугольника MAD.
Проведем прямую KL ║ BC в ΔMBC. Т.к. BC ║ AD, то KL ║ AD и следовательно прямая KL проходящая через точку K и будет одной из сторон сечения.
Окончательно соединяем точки P и L лежащие в одной плоскости и получаем сечение NKLP.
Т.к. KL ║ AD и NP ║ AD, то KL ║ NP и следовательно NKLP - трапеция.
ΔDMC = ΔAMB (т.к. пирамида правильная) ⇒ ∠DMC = ∠AMB
PM = NM (т.к. ΔDMA равносторонний и NP ║ AD)
LM = KM (т.к. ΔBMC равносторонний и KL ║ BC)
Тогда ΔPML = ΔNMK (по двум сторонам и углу между ними).
Следовательно PL = NK и трапеция NKLP - равнобедренная.
Одно из оснований трапеции PN = 3, т.к. является средней линией в ΔAMD с основанием AD = 6
Второе основание KL = 5, т.к. ΔBMC ≈ ΔKML (по трем углам) с коэффициентом подобия 6/5
Найдем боковую сторону трапеции PL из ΔPML, в котором ∠PML = 60°, PM = 3, LM = 5 по теореме косинусов:
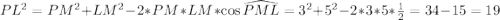
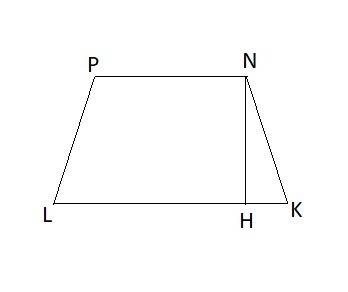
Найдем высоту NH трапеции NKLP. Т.к. трапеция равнобедренная, то
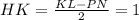
Из прямоугольного ΔNHK
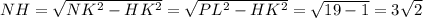
Окончательно находим площадь сечения:
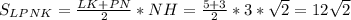
Окружность №1: x²+y²=1. Центр (0; 0), радиус 1.
Окружность №2: x²+(y-7)²=4. Центр (0; 7), радиус 2.
Для удобства и полного понимания ситуации строим данные окружности (изображение 1). Рассмотрим все возможные варианты:
1) Окружность касается обоих данных окружностей внешним образом (изображение 2). В таком случае ее центр (0; 3), радиус 2.
x²+(y-3)²=4
2) Окружность касается обоих данных окружностей внутренним образом (изображение 3). В таком случаем ее центр (0; 4), радиус 5.
x²+(y-4)²=25
3) Окружность касается первой окружности внутренним образом, второй внешним (изображение 4). В таком случае ее центр (0; 2), радиус 3.
x²+(y-2)²=9
4) Окружность касается первой окружности внешним образом, второй внутренним (изображение 5). В таком случае ее центр (0; 5), радиус 4.
x²+(y-5)²=16