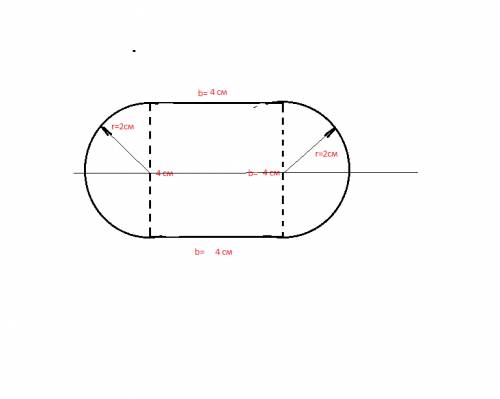
сделаем построение по условию
сторона квадрата b= 4см
диаметр окружности d=b=4см
радиус окружности r=d/2=4/2=2 см
периметр состоит
из двух сторон квадрата 2*b=2*4=8
и
из двух полуокружностей L/2 с радиусом r=2 см
две полуокружности - это полная окружность
длина окружности L=2п*r
Периметр Р=2*b+2*L/2=2b+L=2*4+2п*r=8+2*п*2=8+4*3.14=20,56 см
площадь состоит
из площади квадрата Sкв=b^2
и
из площадей двух полукругов Sкр / 2 = п*r^2 / 2
площадь S=Sкв + 2*Sкр / 2 =Sкв + Sкр = b^2 +п*r^2 = 4^2 + п*2^2 = 16+3.14*4 =28,56 см2
ОТВЕТ
площадь 28,56 см2
Периметр 20,56 см
Площадь круга равна πr², r - это радиус вписанного круга.
Этот радиус легко найти, он равен высоте, проведенной к стороне ромба из точки пересечения диагоналей . Диагонали делят ромб на 4 равных прямоугольных треугольника. Раз один угол в ромбе 60°, то другой 120°, диагонали ромба являются биссектрисами его внутренних углов. Поэтому диагонали делят ромб на треугольники с углами 90°; 60°; 30°. Против угла в 30° лежит катет, равный половине стороны ромба, которая в этом треугольнике является гипотенузой. Поэтому катет равен 5 см. Высоту треугольника ,проведенную к стороне ромба, ищем из треугольника с гипотенузой 5 см, и противолежащим углом в 60Град., т.е. она равна 5sin60град. =
5*√3/2, Площадь круга равна π *25*3/4=75π/4=18,75π/см²/
ответ 18,75π см²