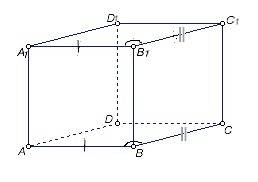
Определение: Параллелепипед — многогранник, у которого шесть граней и каждая из них — параллелограмм.
Требуется доказать, что противоположные грани параллелепипеда параллельны и равны.
Докажем на примере оснований АВСD и A1B1C1D1 данного параллелепипеда.
Отрезки А1В1 и АВ параллельны и равны как стороны параллелограмма АА1В1В, отрезки В1С1 и ВС параллельны и равны как стороны параллелограмма ВСС1В1. ⇒
плоскости оснований параллельны по двум пересекающимся прямым.А1В1 и В1С1 одной плоскости и АВ и ВС противоположной.
Стороны параллелограммов АВСD и A1B1C1D1 равны , соответственные стороны углов А1B1C1 и ABC образованы параллельными прямыми,⇒ углы равны – эти параллелограммы равны, (их можно совместить наложением). Аналогично доказывается параллельность и равенство остальных граней. Доказано.
Sпол=552см²
V=1264√3/3 см³
Объяснение:
Sбок=1/2*(Росн1+Росн2)*ап.
Росн1=А1В1*4=6*4=24см
Росн2=АВ*4=14*4=56см
Sбок=1/2*(24+56)*8=1/2*80*8=320см²
Sосн1=А1В1²=6²=36см²
Sосн2=АВ²=14²=196см²
Sпол=Sбок+Sосн1+Sосн2=320+36+196=
=552см².
МК=8см апофема.
ОМ=В1С1=6см
ТК=ВС=14см.
Трапеция равнобокая.
ТL=PK
PK=(TK-OM)/2=(14-6)/2=4см проекция апофемы на плоскость
∆МРК- прямоугольный треугольник.
По теореме Пифагора
МР=√(МК²-РК²)=√(8²-4²)=√(64-16)=√48=
=4√3 см высота пирамиды.
h=4√3см
V=1/3h(Sосн1+√(Sосн1*Sосн2)+Sосн2)=
=1/3*4√3(36+√(36*196)+196)=
=1/3*4√3*(36+84+196)=4√3/3*316=
=1264√3/3см³