Задача 1
Радиусы перпендикулярны касательным по св-ву касательных.
Рассмотрим прямоугольные треугольники СОВ и СОА.
а) СВ=СА (по св-ву касательных)
б) СО - общая
Вывод: треугольники равны по гипотенузе и катету.
Тогда углы СОА и СОВ равны как соотв. эл-ты.
Угол СОА + угол АСО = 90 градусов
Угол СОА = 90 градусов - (76 градусов : 2) = 52 градуса
Угол АОВ = 2 * угол СОА = 104 градуса
Задача 2
Сумма этих двух углов не равна 180 градусов, тогда они расположены не напротив друг друга. Угол, лежащий напротив угла в 112 градусов равен 180-112=68 градусов.
(Задача решена по условию вписания чет-ка в окр-ть: когда суммы его противположных углов равна по 180 градусов)
Проведем высоту к основанию равнобедренного треугольника. Высота поделит основание на две равные части, т.е. 18/2=9.
Когда мы провели высоту (она же медиана, кстати), у нас образовалось два прямоугольных треугольника. Э ти треугольники будут равны, т.к. гипотенузы уних и катеты равны.
Площадь одного треугольника найдем по теореме Пифагора
41^2=9^2(половина основания большого треугольника)+x^2(х- высота)
х=40.
40 и 9 - катеты тр. S= половина произведения катетов (40*9)/2=180.
Т.к. прямоугольные тр. равны, то площадь большого треугольника равна: 2*180=360.
ответ:360!
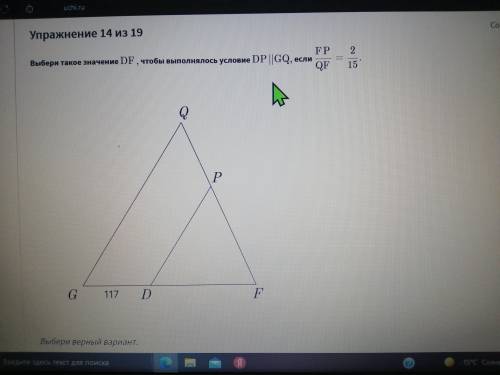
DF=18, строится на подобии трегуольников все